Lecture 10: Sparse direct solvers¶

Recap of the previous lecture¶

Distributed memory for huge dense matrices
Sparse matrix formats (COO, CSR, CSC)
Matrix-by-vector product
Inefficiency of sparse matrix processing
Approaches to reduce cache misses
Fill-in of the sparse matrix

Today lecture¶

Sparse direct solvers:

nested dissection
spectral clustering in details

Fill-in¶

Reminder from the last lecture:

The fill-in of a matrix are those entries which change from an initial zero to a nonzero value during the execution of an algorithm.

Gaussian elimination for sparse matrices¶

Given matrix $A=A^*>0$ we calculate its Cholesky decomposition $A = LL^*$.

Factor $L$ can be dense even if $A$ is sparse:

$$ \begin{bmatrix} * & * & * & * \\ * & * & & \\ * & & * & \\ * & & & * \end{bmatrix} = \begin{bmatrix} * & & & \\ * & * & & \\ * & * & * & \\ * & * & * & * \end{bmatrix} \begin{bmatrix} * & * & * & * \\ & * & * & * \\ & & * & * \\ & & & * \end{bmatrix} $$

How to make factors sparse, i.e. to minimize the fill-in?

Gaussian elimination and permutation¶

We need to find a permutation of indices so that factors are sparse, i.e. we build Cholesky factorisation of $PAP^\top$, where $P$ is a permutation matrix.

For the example from the previous slide

$$ P \begin{bmatrix} * & * & * & * \\ * & * & & \\ * & & * & \\ * & & & * \end{bmatrix} P^\top = \begin{bmatrix} * & & & * \\ & * & & * \\ & & * & * \\ * & * & * & * \end{bmatrix} = \begin{bmatrix} * & & & \\ & * & & \\ & & * & \\ * & * & * & * \end{bmatrix} \begin{bmatrix} * & & & * \\ & * & & * \\ & & * & * \\ & & & * \end{bmatrix} $$

where

$$ P = \begin{bmatrix} & & & 1 \\ & & 1 & \\ & 1 & & \\ 1 & & & \end{bmatrix} $$

Arrowhead form of the matrix gives sparse factors in LU decomposition

In [45]:

import numpy as np
import scipy.sparse as spsp
import scipy.sparse.linalg as spsplin
import scipy.linalg as splin
import matplotlib.pyplot as plt
%matplotlib inline

A = spsp.coo_matrix((np.random.randn(10), ([0, 0, 0, 0, 1, 1, 2, 2, 3, 3], 
                                           [0, 1, 2, 3, 0, 1, 0, 2, 0, 3])))
print("Original matrix")
plt.spy(A)
plt.show()
lu = spsplin.splu(A.tocsc(), permc_spec="NATURAL")
print("L factor")
plt.spy(lu.L)
plt.show()
print("U factor")
plt.spy(lu.U)
plt.show()
print("Column permutation:", lu.perm_c)
print("Row permutation:", lu.perm_r)

Original matrix

L factor

U factor

Column permutation: [0 1 2 3]
Row permutation: [1 2 0 3]

Block arrowhead structure¶

$$ PAP^\top = \begin{bmatrix} A_{11} & & A_{13} \\ & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33}\end{bmatrix} $$

then

$$ PAP^\top = \begin{bmatrix} A_{11} & 0 & 0 \\ 0 & A_{22} & 0 \\ A_{31} & A_{32} & A_{33} - A_{31}A_{11}^{-1} A_{13} - A_{32}A_{22}^{-1}A_{23} \end{bmatrix} \begin{bmatrix} I & 0 & A_{11}^{-1}A_{13} \\ 0 & I & A_{22}^{-1}A_{23} \\ 0 & 0 & I\end{bmatrix} $$

Block $ A_{33} - A_{31}A_{11}^{-1} A_{13} - A_{32}A_{22}^{-1}A_{23}$ is Schur complement for block diagonal matrix $\begin{bmatrix} A_{11} & 0 \\ 0 & A_{22} \end{bmatrix}$
We reduce problem to solving smaller linear systems with $A_{11}$ and $A_{22}$

How can we find permutation?¶

Key idea comes from graph theory
Sparse matrix can be treated as an adjacency matrix of a certain graph: the vertices $(i, j)$ are connected, if the corresponding matrix element is non-zero.

Example¶

Graphs of $\begin{bmatrix} * & * & * & * \\ * & * & & \\ * & & * & \\ * & & & * \end{bmatrix}$ and $\begin{bmatrix} * & & & * \\ & * & & * \\ & & * & * \\ * & * & * & * \end{bmatrix}$ have the following form:

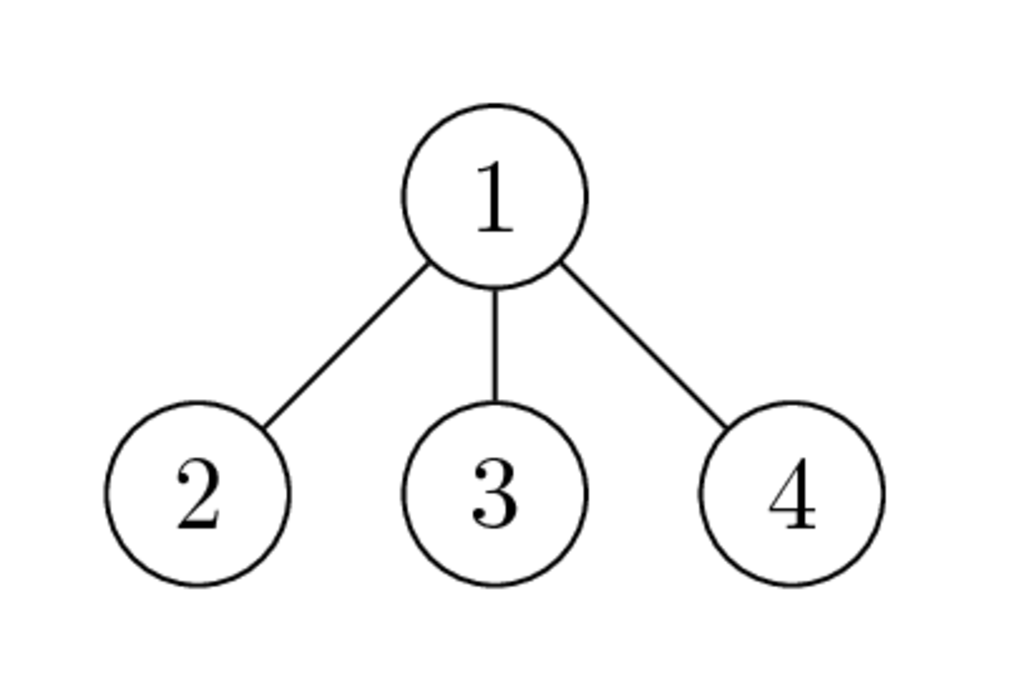and

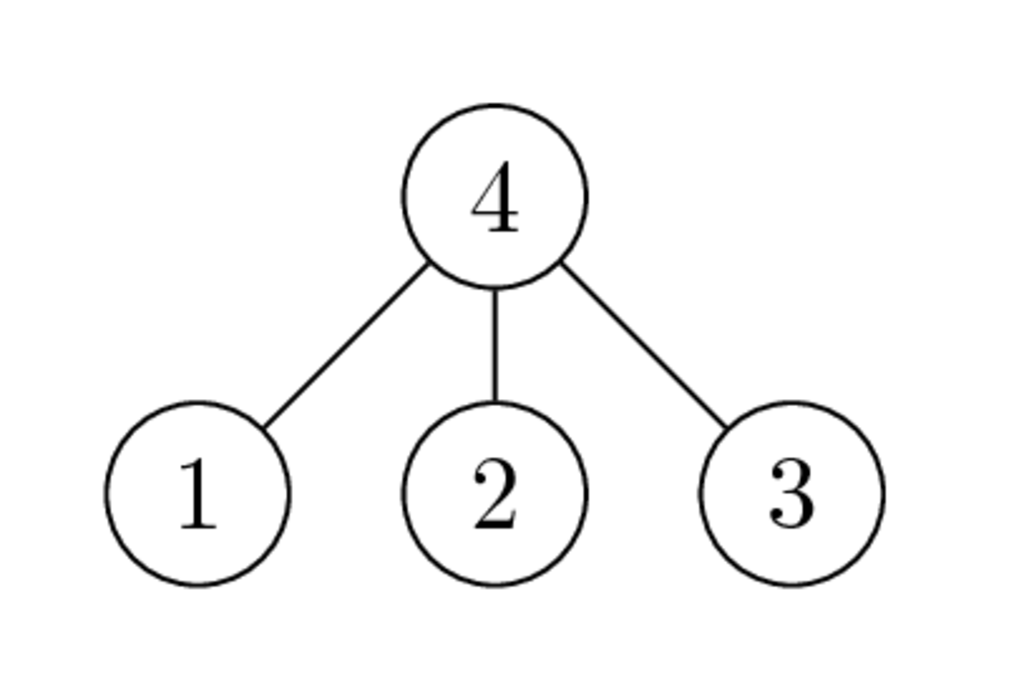
Why the second ordering is better than the first one?

Graph separator¶

Definition. A separator in a graph $G$ is a set $S$ of vertices whose removal leaves at least two connected components.

Separator $S$ gives the following ordering for an $N$-vertex graph $G$:

Find a separator $S$, whose removal leaves connected components $T_1$, $T_2$, $\ldots$, $T_k$
Number the vertices of $S$ from $N − |S| + 1$ to $N$
Recursively, number the vertices of each component: $T_1$ from $1$ to $|T_1|$, $T_2$ from $|T_1| + 1$ to $|T_1| + |T_2|$, etc
If a component is small enough, enumeration in this component is arbitrarily

Separator and block arrowhead structure: example¶

Separator for the 2D Laplacian matrix

$$ A_{2D} = I \otimes A_{1D} + A_{1D} \otimes I, \quad A_{1D} = \mathrm{tridiag}(-1, 2, -1), $$

is as follows

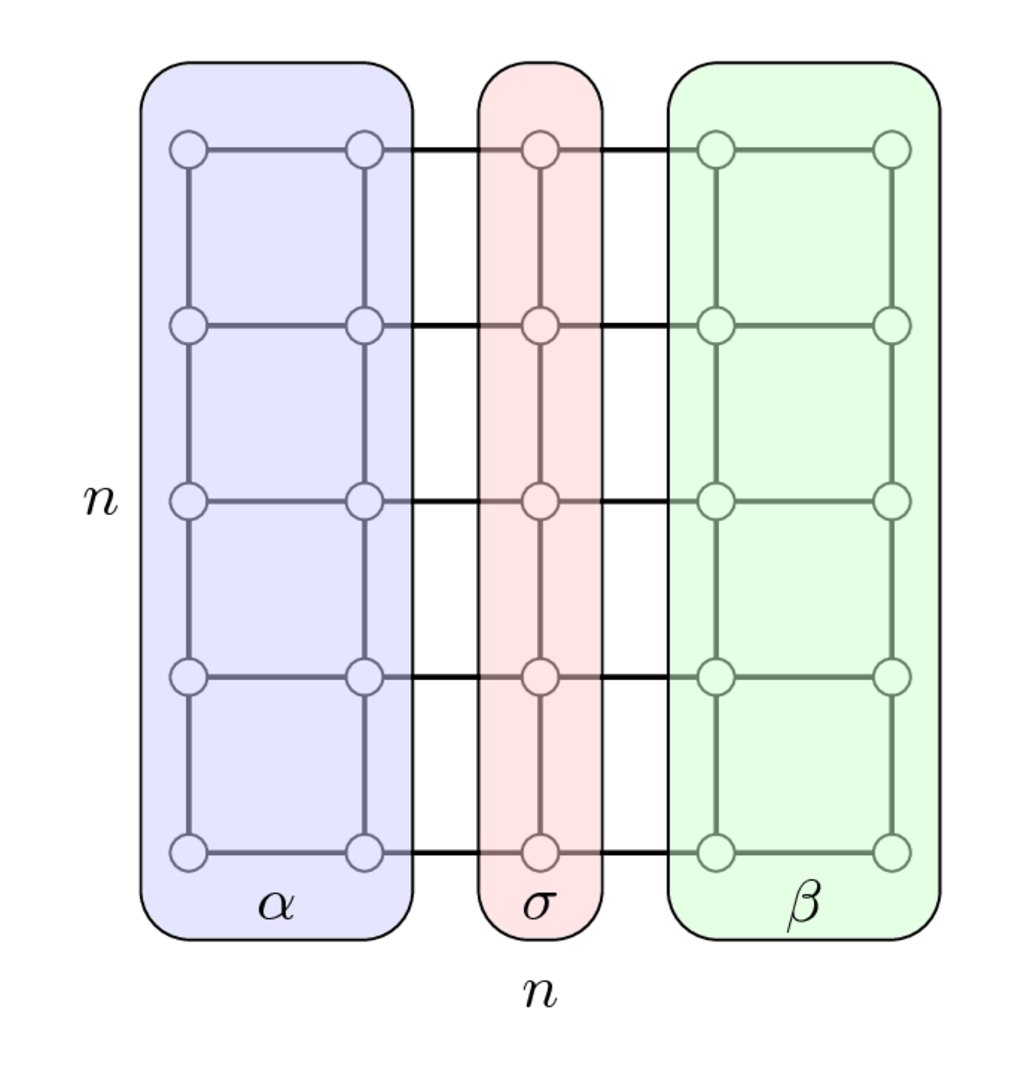
Once we have enumerated first indices in $\alpha$, then in $\beta$ and separators indices in $\sigma$ we get the following matrix

$$ PAP^\top = \begin{bmatrix} A_{\alpha\alpha} & & A_{\alpha\sigma} \\ & A_{\beta\beta} & A_{\beta\sigma} \\ A_{\sigma\alpha} & A_{\sigma\beta} & A_{\sigma\sigma}\end{bmatrix} $$

which has arrowhrad structure.

Thus, the problem of finding permutation was reduced to the problem of finding graph separator!

Nested dissection¶

For blocks $A_{\alpha\alpha}$, $A_{\beta\beta}$ we continue splitting recursively.
When the recursion is done, we need to eliminate blocks $A_{\sigma\alpha}$ and $A_{\sigma\beta}$.
This makes block in the position of $A_{\sigma\sigma}\in\mathbb{R}^{n\times n}$ dense.

Calculation of Cholesky of this block costs $\mathcal{O}(n^3) = \mathcal{O}(N^{3/2})$, where $N = n^2$ is the total number of nodes.

So, the complexity is $\mathcal{O}(N^{3/2})$

Packages for nested dissection¶

MUltifrontal Massively Parallel sparse direct Solver (MUMPS)
Pardiso
Umfpack as part of SuiteSparse

All of them have interface for C/C++, Fortran and Matlab

Nested dissection summary¶

Enumeration: find a separator.
Divide-and-conquer paradigm
Recursively process two subsets of vertices after separation
In theory, nested dissection gives optimal complexity.
In practice, it beats others only for very large problems.

Separators in practice¶

Computing separators is not a trivial task.
Graph partitioning heuristics has been an active research area for many years, often motivated by partitioning for parallel computation.

Existing approaches:

Spectral partitioning (uses eigenvectors of Laplacian matrix of graph) - more details below
Geometric partitioning (for meshes with specified vertex coordinates) review and analysis
Iterative-swapping ((Kernighan-Lin, 1970), (Fiduccia-Matheysses, 19820)
Breadth-first search (Lipton, Tarjan 1979)
Multilevel recursive bisection (heuristic, currently most practical) (review and paper). Package for such kind of partitioning is called METIS, written in C, and available here

Spectral graph partitioning¶

The idea of spectral partitioning goes back to Miroslav Fiedler, who studied connectivity of graphs (paper).

We need to split the vertices into two sets.

Consider +1/-1 labeling of vertices and the cost

$$E_c(x) = \sum_{j} \sum_{i \in N(j)} (x_i - x_j)^2, \quad N(j) \text{ denotes set of neighbours of a node } j. $$

We need a balanced partition, thus $$\sum_i x_i = 0 \quad \Longleftrightarrow \quad x^\top e = 0, \quad e = \begin{bmatrix}1 & \dots & 1\end{bmatrix}^\top,$$ and since we have +1/-1 labels, we have $$\sum_i x^2_i = n \quad \Longleftrightarrow \quad \|x\|_2^2 = n.$$

Graph Laplacian¶

Cost $E_c$ can be written as (check why)

$$E_c = (Lx, x)$$

where $L$ is the graph Laplacian, which is defined as a symmetric matrix with

$$L_{ii} = \mbox{degree of node $i$},$$

$$L_{ij} = -1, \quad \mbox{if $i \ne j$ and there is an edge},$$

and $0$ otherwise.

Rows of $L$ sum to zero, thus there is an eigenvalue $0$ and gives trivial eigenvector of all ones.
Eigenvalues are non-negative (why?).

Partitioning as an optimization problem¶

Minimization of $E_c$ with the mentioned constraints leads to a partitioning that tries to minimize number of edges in a separator, while keeping the partition balanced.

We now relax the integer quadratic programming to the continuous quadratic programming

$$E_c(x) = (Lx, x)\to \min_{\substack{x^\top e =0, \\ \|x\|_2^2 = n}}$$

Fiedler vector¶

The solution to the minimization problem is given by the eigenvector (called Fiedler vector) corresponding to the second smallest eigenvalue of the graph Laplacian. Indeed,

$$ \min_{\substack{x^\top e =0, \\ \|x\|_2^2 = n}} (Lx, x) = n \cdot \min_{{x^\top e =0}} \frac{(Lx, x)}{(x, x)} = n \cdot \min_{{x^\top e =0}} R(x), \quad R(x) \text{ is the Rayleigh quotient} $$ Since $e$ is the eigenvector, corresponding to the smallest eigenvalue, on the space $x^\top e =0$ we get the second minimal eigevalue.

The sign $x_i$ indicates the partitioning.

In computations, we need to find out, how to find this second minimal eigenvalue –– we at least know about power method, but it finds the largest. We will discuss iterative methods for eigenvalue problems later in our course.

This is the main goal of the iterative methods for large-scale linear problems, and can be achieved via few matrix-by-vector products.

In [79]:

import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
kn = nx.read_gml('karate.gml')
print("Number of vertices = {}".format(kn.number_of_nodes()))
print("Number of edges = {}".format(kn.number_of_edges()))
nx.draw_networkx(kn) #Draw the graph

Number of vertices = 34
Number of edges = 78

In [94]:

Laplacian = nx.laplacian_matrix(kn).asfptype()
plt.spy(Laplacian, markersize=5)
plt.title("Graph laplacian")
plt.axis("off")
plt.show()
eigval, eigvec = spsplin.eigsh(Laplacian, k=2, which="SM")
print("The 2 smallest eigenvalues =", eigval)

The 2 smallest eigenvalues = [-2.74105525e-15  4.68525227e-01]

In [95]:

plt.scatter(np.arange(len(eigvec[:, 1])), np.sign(eigvec[:, 1]))
plt.show()
print("Sum of elements in Fiedler vector = {}".format(np.sum(eigvec[:, 1].real)))

Sum of elements in Fiedler vector = -1.2878587085651816e-14

In [93]:

nx.draw_networkx(kn, node_color=np.sign(eigvec[:, 1]))

Summary on demo¶

Here we call SciPy sparse function to find fixed number of eigenvalues (and eigenvectors) that are smallest (other options are possible)
Details of the underlying method we will discuss soon
Fiedler vector gives simple separation of the graph
To separate graph on more than two parts you should use eigenvectors of laplacian as feature vectors and run some clustering algorithm, e.g. $k$-means

Fiedler vector and algebraic connectivity of a graph¶

Definition. The algebraic connectivity of a graph is the second-smallest eigenvalue of the Laplacian matrix.

Claim. The algebraic connectivity of a graph is greater than 0 if and only if a graph is a connected graph.

Minimal degree orderings¶

The idea is to eliminate rows and/or columns with fewer non-zeros, update fill-in and then repeat
Efficient implementation is an issue (adding/removing elements).
Current champion is "approximate minimal degree" by Amestoy, Davis, Duff.
It is suboptimal even for 2D problems
In practice, it often wins for medium-sized problems
SciPy sparse package uses minimal ordering approach for different matrices ($A^{\top}A$, $A + A^{\top}$)