Lecture 15: Matrix functions and matrix equations¶

Previous part¶

Toeplitz matrices, circulant matrices, FFT

Today lecture¶

Matrix functions and matrix equations

Outline of this part¶

What is a matrix function
Matrix exponential
(Some) applications

Book to read: Functions of matrices by Nick Higham

The simplest matrix function: matrix polynomial¶

It is very easy to define a matrix polynomial as

$$ P(A) = \sum_{k=0}^n c_k A^k. $$

Side-note: Hamilton-Cayley theorem states that $F(A) = 0$ where $F(\lambda) = \det(A - \lambda I)$, thus all matrix polynomials have degree $\leq n-1$.

Matrix polynomials as building blocks¶

We can define a function of the matrix by Taylor series:

$$ f(A) = \sum_{k=0}^{\infty} c_k A^k. $$

The convergence is understood as the convergence in some matrix norm.

Example of such series is the Neumann series

$$ (I - F)^{-1} = \sum_{k=0}^{\infty} F^k, $$

which is well defined for $\rho(F) < 1$.

Matrix exponential series¶

The most well-known matrix function is matrix exponential. In the scalar case,

$$ e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \ldots = \sum_{k=0}^{\infty} \frac{x^k}{k!}, $$

and it directly translates to the matrix case:

$$ e^A = \sum_{k=0}^{\infty} \frac{A^k}{k!}, $$

the series that always converges, because the series

$$\sum_{k=0}^{\infty} \frac{\Vert A \Vert^k}{k!} = e^{\Vert A \Vert}.$$

Why matrix exponential is important¶

A lot of practical problems are reduced to a system of linear ODEs of the form

$$ \frac{dy}{dt} = Ay, \quad y(0) = y_0. $$

ODE and matrix exponentials¶

Given the equation

$$\frac{dy}{dt} = Ay, \quad y(0) = y_0$$

The formal solution is given by $y(t) = e^{At} y_0$, so if we know $e^{At}$ (or can compute matrix-by-vector product fast) there is a big gain over the time-stepping schemes.
Indeed,

$$\frac{d}{dt} e^{At} = \frac{d}{dt} \sum_{k=0}^{\infty} \frac{t^k A^k}{k!} = \sum_{k=1}^{\infty} \frac{t^{k-1} A^{k}}{(k-1)!} = A e^{At}.$$

Sidenote: matrix exponential and time stepping¶

Matrix exponential can be much better than solving using, say, Euler scheme:

$$\frac{dy}{dt} \approx \frac{y_{k+1} - y_k}{\tau} = A y_k, \quad y_{k+1} = y_k + \tau A y_k,$$

if we know how to compute the product of the matrix exponential by vector using only matrix-by-vector product.

For dense matrices matrix exponential also provides exact answer to the ODE for any $t$, compared to the approximation by time-stepping schemes.

How to compute matrix functions, including exponential?¶

There are many ways, even for the matrix exponential!
See C. Van Loan, C. Moler, Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later
The simplest way is to diagonalize the matrix:

$$ A = S \Lambda S^{-1}, $$

where the columns of $S$ are eigenvectors of the matrix $A$, then

$$ F(A) = S F(\Lambda) S^{-1}. $$

Problem: diagonalization can be unstable! (and not every matrix is diagonalizable)

Let us look how matrices are diagonalizable:

import numpy as np
eps = 1e-4
p = 4
a = np.eye(p)
for i in range(p-1):
    a[i, i+1] = 1
    
a[p-1, 2] = eps

val, vec = np.linalg.eig(a)
#print a
print(np.linalg.norm(a - vec.dot(val[:, np.newaxis] * np.linalg.inv(vec))))
#print 'S * D * S^{-1}:' 
print(vec.dot(val[:, np.newaxis] * np.linalg.inv(vec)))
print(a)

16384.000030517578
[[1.00000000e+00 0.00000000e+00 9.09494702e-13 1.63840000e+04]
 [0.00000000e+00 1.00000000e+00 1.00000000e+00 0.00000000e+00]
 [0.00000000e+00 0.00000000e+00 1.00000000e+00 1.00000000e+00]
 [0.00000000e+00 0.00000000e+00 1.00000000e-04 1.00000000e+00]]
[[1.e+00 1.e+00 0.e+00 0.e+00]
 [0.e+00 1.e+00 1.e+00 0.e+00]
 [0.e+00 0.e+00 1.e+00 1.e+00]
 [0.e+00 0.e+00 1.e-04 1.e+00]]

Now we can compute a function for perturbed Jordan block.

import numpy as np
eps = 1e-16
p = 5
a = np.eye(p)
for i in range(p-1):
    a[i, i+1] = 1
    
a[p-1, 0] = eps
a = np.array(a)
val, vec = np.linalg.eig(a)
print(np.linalg.norm(a - vec.dot(np.diag(val)).dot(np.linalg.inv(vec))))

fun = lambda x: np.exp(x)

#Using diagonalization
fun_diag = vec.dot(np.diag(fun(val))).dot(np.linalg.inv(vec))


#Using Schur
import scipy.linalg
fun_m = scipy.linalg.expm(a)
print('Difference = {}'.format(np.linalg.norm(fun_m - fun_diag)))

2.0
Difference = 5.959978842992802

How `funm` function works¶

The exponential of a matrix is a special function, so there are special methods for its computation.
For a general function $F$, there is a beautiful Schur-Parlett algorithm, which is based on the Schur theorem

Schur-Parlett algorithm¶

Given a matrix $A$ we want to compute $F(A)$, and we only can evaluate $F$ at scalar points.
First, we reduce $A$ to the triangular form as

$$ A = U T U^*. $$

Therefore, $F(A)=U F(T) U^*$
We only need to compute the function of triangular matrices.

Computing functions of triangular matrices¶

We know values on the diagonals

$$ F_{ii} = F(T_{ii}), $$

and also we know that

$$ F T = T F $$

the matrix function commutes with the matrix itself. The function of a triangular matrix is a triangular matrix as well. Using the known values on the diagonal and the commutativity property, we get the diagonals of the matrix one-by-one:

$$f_{ij} = t_{ij} \frac{f_{ii} - f_{jj}}{t_{ii} - t_{jj}} + \sum_{k=i+1}^{j-1} \frac{f_{ik} t_{kj} - t_{ki}f_{kj}}{t_{ii} - t_{jj}}.$$

Matrix functions: definition¶

One way to define a matrix function $f(A)$ is to use Jordan canonical form.
A much more elegant way is to use Cauchy integral representation:

$$ f(A) = \int_{\Gamma} f(z) (zI - A)^{-1} dz, $$

]where $f(z)$ is analytic on and inside a closed contour $\Gamma$ that encloses the spectrum of $A$.

This definition can be generalized to the operator case.

Important matrix functions¶

Matrix exponential, used to solve $\frac{dy}{dt} = Ay$ in the "explicit" way, $y = y_0 e^{At}.$
$\cos(A), \sin(A)$ used to solve wave equation $\frac{d^2 y}{dt^2} + Ay = 0.$
Sign function, $\mathrm{sign}(A)$, used to compute spectral projections.
Inverse square root $A^{-1/2}$ used in many places, for example, to generate samples from a Gaussian distributions

Matrix exponential¶

The matrix exponential is given by the following series:

$$e^A = I + A + \frac{1}{2} A^2 + \frac{1}{3!} A^3 + \ldots$$

This series is a bad idea (even for a scalar case, can you guess why?)
This form for $e^A$ almost assumes a Krylov method for the evaluation of $e^{At} y_0,$ by the way.

import numpy as np

x = -30.0 #Point
k = 1000000 #Number of terms
b = 1.0
x0 = x
for i in range(1, k):
    b += x0
    x0 *= x/(i+1)
    
print('Error in the exponent: {}'.format((b - np.exp(x))/np.exp(x)))

Error in the exponent: 65220007.32064143

Series convergence¶

The series convergence for the matrix exponential can be slow for large $x!$ (and slow for big norm).
What we can do?

Method 1: Krylov method¶

We can use the idea of Krylov method: using the Arnoldi method, generate the orthogonal basis in the Krylov subspace, and compute (it can be used in general for any function)

$$ f(A)v \approx f(Q H Q^*)v = Q f(H) Q^*v,$$

where $H$ is a small upper Hessenberg matrix, for which we can use, for example, the Schur-Parlett algorithm.

The convergence of the Krylov method can be quite slow: it is actually a polynomial approximation to a function.
And convergence of polynomial approximation to the matrix function can be slow.
Idea: Replace by rational approximation!

Pade approximations¶

Matrix exponential is well approximated by rational function:

$$ \exp(x) \approx \frac{p(x)}{q(x)}, $$

where $p(x)$ and $q(x)$ are polynomials and computation of a rational function of a matrix is reduced to matrix-matrix products and matrix inversions.

The rational form is also very useful when only a product of a matrix exponential by vector is needed, since evaluation reduces to matrix-by-vector products and linear systems solvers

#Computing Pade approximant
import numpy as np
import mpmath
%matplotlib inline
from mpmath import pade, taylor, polyval
import matplotlib.pyplot as plt
x = np.linspace(-5, -1, 128)
a = taylor(mpmath.exp, 0, 20) #Taylor series
k1 = 10
k2 = 10
p, q = pade(a, k1, k2) #Pade approximant
#plt.plot(x, polyval(p[::-1], x)/polyval(q[::-1], x) - np.exp(x))
plt.semilogy(x, polyval(a[::-1], x) - np.exp(x))

_ = plt.title('Error of the Pade of order {0:d}/{1:d}'.format(k1, k2) )

Scaling & squaring algorithm¶

The "canonical algorithm" for the computation of the matrix exponential also relies on scaling of the matrix $A:$

$$\exp(A) = \exp(A/2^k)^{(2^k)}.$$

The matrix then can have a small norm, thus:

Scale the matrix as $B := A/2^k$ to make it norm less than $1$.
Compute exponent of $C = e^B$ by a Pade approximant
Square $e^A \approx C^{(2^k)}$ in $k$ matrix-by-matrix products.

Large-scale matrix exponentials¶

Large-scale matrices obviously do not allow for efficient scaling-and-squaring (need to work with dense matrices), thus we can use Krylov methods or (better) Rational Krylov methods.
The idea of a rational Krylov subspace is motivated by the idea of rational approximation instead of polynomial approximation.
Krylov methods rely on polynomial approximations

Rational Krylov subspaces¶

The simplest (yet efficient) approach is based on the so-called extended Krylov subspaces:

$$KE(A, b) = \mathrm{Span}(\ldots, A^{-2} b, A^{-1} b, b, A b, A^2 b, \ldots)$$

At each step you add a vector of the form $A w$ and $A^{-1} w$ to the subspace, and orthogonalize the result (rational Arnoldi method).

I.e., we need only linear system solver for one step, but since the matrix $A$ is fixed, we can factorize it once

Rational Krylov methods¶

Rational Krylov methods are the most efficient for the computation of matrix functions:

we construct an orthogonal basis in the span,

$$KE(A, b) = \mathrm{Span}(\ldots, A^{-2} b, A^{-1} b, b, A b, A^2 b, \ldots)$$

compute

$$f(A)b \approx Q f(H) Q^*b,$$

where $H = Q^* A Q.$

It requires one solver and matrix-by-vector product at each step.

Application to compute distance between manifolds¶

Represent two manifolds $\mathcal{M}$ and $\mathcal{N}$ with point clouds
Construct two graphs from these point clouds
Every graph has its own graph laplacian ($L_{\mathcal{M}}$ and $L_{\mathcal{N}}$) (check the lecture about Fiedler vector!)
Heat kernel trace

$$\mathrm{hkt}_{\mathcal{M}}(t) = \mathrm{trace}(\exp(-t L_{\mathcal{M}}))$$

contains all information about graph's spectrum

Gromov-Wasserstein distance between manifolds $\mathcal{M}$ and $\mathcal{N}$:

$$d_{GW}(\mathcal{M}, \mathcal{N}) \geq \sup_{t > 0} \exp(-2(t + t^{-1}))|\mathrm{hkt}_{\mathcal{M}}(t) - \mathrm{hkt}_{\mathcal{N}}(t)|$$

Stochastic trace estimator¶

Hutchinson proposes the following method

$$ \mathrm{trace}(A) = \mathbb{E}_{p(x)}(x^{\top}Ax), $$

where $p(x)$ is distribution with zero mean and unit variance, e.g. Rademacher or standard normal distributions

To estimate trace we need the fast matrix by vector product!
And here the rational Krylov subspace helps a lot since $\mathrm{hkt}$ requires trace of matrix exponential

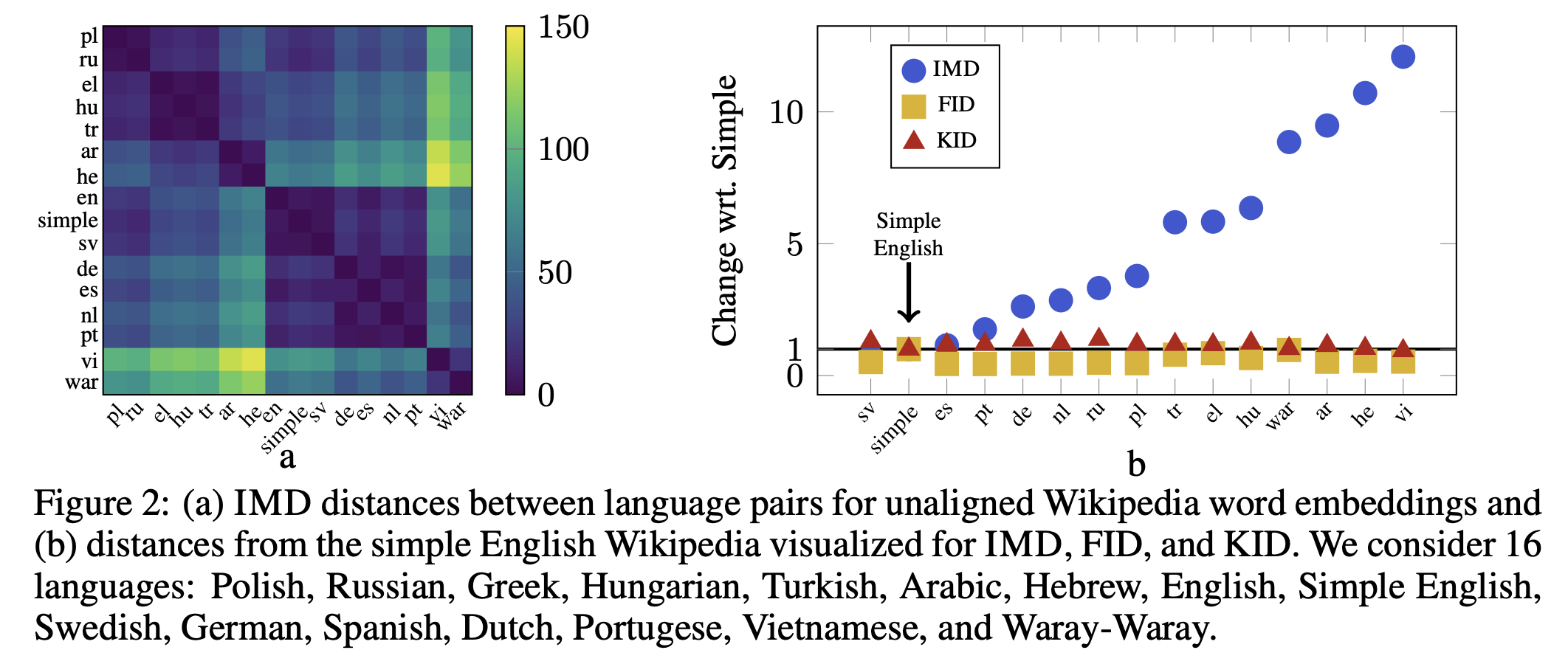
Distances between languages (original paper)¶

Other matrix functions¶

Now, let us briefly talk about other matrix functions:

sign
inverse square root

Sign function¶

Sign function is defined as

$$\mathrm{sign}(x) = \begin{cases} 1, \quad x > 0, \\ -1, \quad x < 0. \end{cases}$$

Given a matrix $A = U \Lambda U^*$, it effectively puts all the eigenvalues larger than $0$ to $1$, and all eigenvalues smaller than $0$ to $-1$, thus

$$P = \frac{(I + \mathrm{sign}(A))}{2}$$

is a projector onto the subspace spanned by all positive eigenvalues.

Such projectors can be very useful in large-scale eigenvalue computations, when you only need to find a subspace.

How to compute sign function?¶

There is a very simple iteration to compute the sign function, namely

$$X_{k+1} = \frac{1}{2} (X_k + X^{-1}_k), X_0 = \alpha A.$$

This iteration converges quadratically to the sign function.
You can also get a polynomial iteration, proposed by R. Byers

$$X_{k+1} = \frac{1}{2} X_k (3 I - X_k), \quad X_0 = \alpha A.$$

Matrix sign function: applications¶

One of the important applications of the matrix sign function is the solution of the Algebraic Riccati equation

$$A^* X + X A - X R X + G = 0,$$

which arises in optimal control and stochastic control.

Solving ARE is equivalent to finding a stable invariant subspace (i.e., corresponding to the negative eigenvalues) of the matrix

$$ C = \begin{bmatrix} A^* & G \\ R & -A \end{bmatrix}. $$

Inverse square root of the matrix¶

The inverse square root of the matrix, $A^{-1/2}$ is also often important.
For example, the multidimensional Gaussian distribution with covariance matrix $A = A^* > 0$ is given by the

$$e^{A^{-1} x, x}.$$

Suppose $x$ is really huge (millions), how we generate samples, given a structured matrix $A$?
The simplest algorithm is to generate a normally distributed vector $y$ with $y_i$ from $N(0, 1)$, and then compute

$$x = A^{-\frac{1}{2}} y.$$

The vector $x$ will have the desired distribution.
To compute matrix square root it is very efficient to use rational Krylov subspaces.

Matrix equations¶

An equation of the form

$$F(X) = G, \quad X \in \mathbb{R}^{n \times m}$$

is called matrix equation.

A linear matrix equation is when $X$ and $G$ are matrices, and $F$ is a linear operator.

Two important matrix equations¶

We will discuss two matrix equations:

Sylvester equation of the form

$$ A X + X B = C,$$

where $A$ and $B$ are given, and its special case, continious Lyapunov equation,

$$ A X + XA^{\top} = C,$$

and

discrete Lyapunov equation

$$A X A^* - X = C. $$

Application of the Lyapunov equation¶

Lyapunov equation is very important for the stability of dynamical systems, and also for model order reduction.

$$\frac{dy}{dt} = Ay, \quad y(0) = y_0,$$$$y(t) \rightarrow 0$$

for $t \rightarrow \infty$.

System is stable, iff for any $Q = Q^* > 0$ there exists a unique positive definite solution $P$ of the Lyapunov equation

$$A P + P A^* = Q.$$

The stability then can be checked without finding eigenvalues.

Application to model order reduction¶

Model order reduction of linear time-invariant systems:

$$\frac{dx}{dt} = Ax + Bu, \quad y = C x,$$

where $x$ is state, $u$ is control, and $y$ is the observable. We want to approximate it by a smaller-dimensional linear system

$$ \frac{d\widehat{x}}{dt} = \widehat{A} \widehat{x} + \widehat{B} u, \quad y = \widehat{C} \widehat{x}, $$

in such a way that the output of the reduced system is close to the output of the original (big one).

The optimal $\widehat{A}, \widehat{B}, \widehat{C}$ can be recovered from the solution of the auxiliary Lyaupunov equations.

Solution of the Sylvester equation¶

$$ A X + X B = C,$$

This is a system of linear equations for $X$.
It can be rewritten as a linear system using the vec and Kronecker product operations.
First, we introduce the $\mathrm{vec}$ operation by taking the element of a matrix into a one long vector.

Kronecker product¶

A Kronecker product of two matrices $A \in \mathbb{R}^{n_1 \times m_1}, \quad B \in \mathbb{R}^{n_2 \times m_2}$ is a matrix $C$ of size $(n_1 n_2) \times (m_1 m_2)$.

Of the block form

$$A \otimes B = [a_{ij} B].$$

Main property of the Kronecker product and vec¶

We have

$$\mathrm{vec}(A X B^{\top}) = (B \otimes A) \mathrm{vec}(X).$$

Rewriting the Sylvester equation¶

$$\mathrm{vec}(A X B^{\top}) = (B \otimes A) \mathrm{vec}(X).$$

We can use it to rewrite the Sylvester equation

$$ A X + X B = C $$

in the form

$$\mathrm{vec}(AX + X B) = (I \otimes A + B^{\top} \otimes I) \mathrm{vec}(X) = \mathrm{vec}(C).$$

Thus, we need to solve a linear system with the matrix

$$(I \otimes A + B^{\top} \otimes I)$$

It is a matrix of size $n^2$, thus Gaussian elimination will take $\mathcal{O}(n^6)$ operations.
We can do it in $\mathcal{O}(n^3)$ operations!

Solving Sylvester equation: Bartels-Stewart method¶

$$(I \otimes A + B^{\top} \otimes I) x = c.$$

Let us compute Schur decomposition of $A$ and $B$:

$$A = Q_A T_A Q^*_A, \quad B^{\top} = Q_B T_B Q^*_B.$$

Then, we have

$$(I \otimes A + B^{\top} \otimes I) = (I \otimes ( Q_A T_A Q^*_A ) + (Q_B T_B Q^*_B \otimes I) = (Q_B \otimes Q_A) ( I \otimes T_A + T_B \otimes I) (Q^* _B \otimes Q^*_A). $$