import jax.numpy as jnp
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
kn = nx.read_gml('karate.gml')
#nx.write_gml(kn, 'karate2.gml')
nx.draw_networkx(kn, node_color="red") #Draw the graph
Today we will talk about:
The number $\lambda$ is called an eigenvalue. The name eigenpair is also used.
Since $A - \lambda I$ should have a non-trivial kernel, eigenvalues are the roots of the characteristic polynomial
If matrix $A$ of size $n\times n$ has $n$ eigenvectors $s_i$, $i=1,\dots,n$:
$$ As_i = \lambda_i s_i, $$then this can be written as
$$ A S = S \Lambda, \quad\text{where}\quad S=(s_1,\dots,s_n), \quad \Lambda = \text{diag}(\lambda_1, \dots, \lambda_n), $$or equivalently
$$ A = S\Lambda S^{-1}. $$What classes of matrices are diagonalizable?
Simple example can be matrices with all different eigenvalues.
More generally, matrix is diagonalizable iff algebraic multiplicity of each eigenvalue (mutiplicity of eigenvalue in the characteristic polynomial) is equal to its geometric multiplicity (dimension of eigensubspace).
For our purposes the most important class of diagonalizable matrices is the class of normal matrices:
has one eigenvalue $1$ of multiplicity $2$ (since its characteristic polynomial is $p(\lambda)=(1-\lambda)^2$), but only one eigenvector $\begin{pmatrix} c \\ 0 \end{pmatrix}$ and hence the matrix is not diagonalizable.
Can you give some examples?
A typical computation of eigenvectors / eigenvectors is for studying
from IPython.display import YouTubeVideo
YouTubeVideo("VcCcMZo6J6w")
where $L(j)$ is the number of outgoing links on the $j$-th page, $N(i)$ are all the neighbours of the $i$-th page. It can be rewritten as
$$ p = G p, \quad G_{ij} = \frac{1}{L(j)} $$or as an eigenvalue problem
i.e. the eigenvalue $1$ is already known. Note that $G$ is left stochastic, i.e. its columns sum up to $1$. Check that any left stochastic matrix has maximum eigenvalue equal to $1$.
networkx package for working with graphs that can be installed using conda install networkx
import jax.numpy as jnp
%matplotlib inline
import matplotlib.pyplot as plt
import networkx as nx
kn = nx.read_gml('karate.gml')
#nx.write_gml(kn, 'karate2.gml')
nx.draw_networkx(kn, node_color="red") #Draw the graph
pr = nx.algorithms.link_analysis.pagerank(kn)
pr_vector = list(pr.values())
pr_vector = jnp.array(pr_vector) * 3000
nx.draw_networkx(kn, node_size=pr_vector, node_color="red", labels=None)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
There are two types of eigenproblems:
The eigenvalue problem has the form
$$ Ax = \lambda x, $$or
$$ (A - \lambda I) x = 0, $$therefore matrix $A - \lambda I$ has non-trivial kernel and should be singular.
That means, that the determinant
$$ p(\lambda) = \det(A - \lambda I) = 0. $$The determinant of a square matrix $A$ is defined as
$$\det A = \sum_{\sigma \in S_n} \mathrm{sgn}({\sigma})\prod^n_{i=1} a_{i, \sigma_i},$$where
Determinant has many nice properties:
1. $\det(AB) = \det(A) \det(B)$
2. If we have one row as a sum of two vectors, determinant is a sum of two determinants
3. "Minor expansion": we can expand determinant through a selected row or column.
If you do it via minor expansion, we get exponential complexity in $n$.
Can we do $\mathcal{O}(n^3)$?
Now we go back to the eigenvalues.
The characteristic equation can be used to compute the eigenvalues, which leads to naïve algorithm:
Is this a good idea?
Give your feedback
We can do a short demo of this
import numpy as jnp
import jax
n = 40
a = [[1.0 / (i - j + 0.5) for i in range(n)] for j in range(n)]
a = jnp.array(a)
ev = jnp.linalg.eigvals(a)
#There is a special numpy function for chacteristic polynomial
cf = jnp.poly(a)
ev_roots = jnp.roots(cf)
#print('Coefficients of the polynomial:', cf)
#print('Polynomial roots:', ev_roots)
plt.scatter(ev_roots.real, ev_roots.imag, marker='x', label='roots')
b = a + 0 * jax.random.normal(jax.random.PRNGKey(0,), (n, n))
ev_b = jnp.linalg.eigvals(b)
plt.scatter(ev_b.real, ev_b.imag, marker='o', label='Lapack')
#plt.scatter(ev_roots.real, ev_roots.imag, marker='o', label='Brute force')
plt.legend(loc='best')
plt.xlabel('Real part')
plt.ylabel('Imaginary part')
Text(0, 0.5, 'Imaginary part')
is the Hilbert matrix, which has exponential decay of singular values.
There is a very interesting theorem that sometimes helps to localize the eigenvalues.
It is called Gershgorin theorem.
It states that all eigenvalues $\lambda_i, i = 1, \ldots, n$ are located inside the union of Gershgorin circles $C_i$, where $C_i$ is a disk on the complex plane with center $a_{ii}$ and radius
First, we need to show that if the matrix $A$ is strictly diagonally dominant, i.e.
$$ |a_{ii}| > \sum_{j \ne i} |a_{ij}|, $$then such matrix is non-singular.
We separate the diagonal part and off-diagonal part, and get
$$ A = D + S = D( I + D^{-1}S), $$and $\Vert D^{-1} S\Vert_1 < 1$. Therefore, by using the Neumann series, the matrix $I + D^{-1}S$ is invertible and hence $A$ is invertible.
Now the proof follows by contradiction:
import jax.numpy as jnp
%matplotlib inline
n = 3
fig, ax = plt.subplots(1, 1)
a = [[5, 1, 1], [1, 0, 0.5], [2, 0, 10]]
#a = [[1.0 / (i - j + 0.5) for i in xrange(n)] for j in xrange(n)]
a = jnp.array(a)
#a = np.diag(np.arange(n))
a = a + 2 * jax.random.normal(jax.random.PRNGKey(0), (n, n))
#u = np.random.randn(n, n)
#a = np.linalg.inv(u).dot(a).dot(u)
xg = jnp.diag(a).real
yg = jnp.diag(a).imag
rg = jnp.zeros(n)
ev = jnp.linalg.eigvals(a)
for i in range(n):
rg = jax.ops.index_update(rg, jax.ops.index[i], jnp.sum(jnp.abs(a[i, :])) - jnp.abs(a[i, i]))
crc = plt.Circle((xg[i], yg[i]), radius=rg[i], fill=False)
ax.add_patch(crc)
plt.scatter(ev.real, ev.imag, color='r', label="Eigenvalues")
plt.axis('equal')
plt.legend()
ax.set_title('Eigenvalues and Gershgorin circles')
fig.tight_layout()
Note: There are more complicated figures, like Cassini ovals, that include the spectrum
$$ _{ij} = \{z\in\mathbb{C}: |a_{ii} - z|\cdot |a_{jj} - z|\leq r_i r_j\}, \quad r_i = \sum_{l\not= i} |a_{il}|. $$can be rewritten as a fixed-point iteration.
Power method has the form
$$ x_{k+1} = A x_k, \quad x_{k+1} := \frac{x_{k+1}}{\Vert x_{k+1} \Vert_2}$$and
$$ x_{k+1}\to v_1,$$where $Av_1 = \lambda_1 v_1$ and $\lambda_1$ is the largest eigenvalue and $v_1$ is the corresponding eigenvector.
Note that $\lambda^{(k+1)}$ is not required for the $(k+2)$-th iteration, but might be useful to measure error on each iteration: $\|Ax_{k+1} - \lambda^{(k+1)}x_{k+1}\|$.
The convergence is geometric, but the convergence ratio is $q^k$, where $q = \left|\frac{\lambda_{2}}{\lambda_{1}}\right| < 1$, for $\lambda_1>\lambda_2\geq\dots\geq \lambda_n$ and $k$ is the number of iteration.
Let's have a more precise look at the power method when $A$ is Hermitian. In two slides you will learn that every Hermitian matrix is diagonalizable. Therefore, there exists orthonormal basis of eigenvectors $v_1,\dots,v_n$ such that $Av_i = \lambda_i v_i$. Let us decompose $x_0$ into a sum of $v_i$ with coefficients $c_i$:
$$ x_0 = c_1 v_1 + \dots + c_n v_n. $$Since $v_i$ are eigenvectors, we have
$$ \begin{split} x_1 &= \frac{Ax_0}{\|Ax_0\|} = \frac{c_1 \lambda_1 v_1 + \dots + c_n \lambda_n v_n}{\|c_1 \lambda_1 v_1 + \dots + c_n \lambda_n v_n \|} \\ &\vdots\\ x_k &= \frac{Ax_{k-1}}{\|Ax_{k-1}\|} = \frac{c_1 \lambda_1^k v_1 + \dots + c_n \lambda_n^k v_n}{\|c_1 \lambda_1^k v_1 + \dots + c_n \lambda_n^k v_n \|} \end{split} $$Now you see, that
$$ x_k = \frac{c_1}{|c_1|}\left(\frac{\lambda_1}{|\lambda_1|}\right)^k\frac{ v_1 + \frac{c_2}{c_1}\frac{\lambda_2^k}{\lambda_1^k}v_2 + \dots + \frac{c_n}{c_1}\frac{\lambda_n^k}{\lambda_1^k}v_n}{\left\|v_1 + \frac{c_2}{c_1}\frac{\lambda_2^k}{\lambda_1^k}v_2 + \dots + \frac{c_n}{c_1}\frac{\lambda_n^k}{\lambda_1^k}v_n\right\|}, $$which converges to $v_1$ since $\left| \frac{c_1}{|c_1|}\left(\frac{\lambda_1}{|\lambda_1|}\right)^k\right| = 1$ and $\left(\frac{\lambda_2}{\lambda_1}\right)^k \to 0$ if $|\lambda_2|<|\lambda_1|$.
There is one class of matrices when eigenvalues can be found easily: triangular matrices
$$ A = \begin{pmatrix} \lambda_1 & * & * \\ 0 & \lambda_2 & * \\ 0 & 0 & \lambda_3 \\ \end{pmatrix}. $$The eigenvalues of $A$ are $\lambda_1, \lambda_2, \lambda_3$. Why?
Because the determinant is
$$ \det(A - \lambda I) = (\lambda - \lambda_1) (\lambda - \lambda_2) (\lambda - \lambda_3). $$where we have used the famous multiplicativity property of the determinant, $\det(AB) = \det(A) \det(B)$.
If we manage to make $U^* A U = T$ where $T$ is upper triangular, then we are done.
Multplying from the left and the right by $U$ and $U^*$ respectively, we get the desired decomposition:
This is the celebrated Schur decomposition.
Theorem: Every $A \in \mathbb{C}^{n \times n}$ matrix can be represented in the Schur form $A = UTU^*$, where $U$ is unitary and $T$ is upper triangular.
Sketch of the proof.
where $A_2$ is an $(n-1) \times (n-1)$ matrix. This is called block triangular form. We can now work with $A_2$ only and so on.
Note: Since we need eigenvectors in this proof, this proof is not a practical algorithm.
Important application of the Schur theorem: normal matrices.
Definition. Matrix $A$ is called normal matrix, if
Q: Examples of normal matrices?
Examples: Hermitian matrices, unitary matrices.
Theorem: $A$ is a normal matrix, iff $A = U \Lambda U^*$, where $U$ is unitary and $\Lambda$ is diagonal.
Sketch of the proof:
Therefore, every normal matrix is unitary diagonalizable, which means that it can be diagonalized by unitary matrix $U$.
In other words every normal matrix has orthogonal basis of eigenvectors.
Everything is fine, but how we compute the Schur form?
This will be covered in the next lecture.
and the maximal eigenvalue is the maximum of $R_A(x)$, and the minimal eigenvalue is the minimal of $R_A(x)$.
Now, "advanced" concept.
For linear dynamical systems given by the matrix $A$, spectrum can tell a lot about the system (i.e. stability, ...)
However, for non-normal matrices, spectrum can be unstable with respect to small perturbations.
In order to measure such perturbation, the notion of pseudospectrum has been developed.
We consider the union of all possible eigenvalues of all perturbations of the matrix $A$.
$$\Lambda_{\epsilon}(A) = \{ \lambda \in \mathbb{C}: \exists E, x \ne 0: (A + E) x = \lambda x, \quad \Vert E \Vert_2 \leq \epsilon. \}$$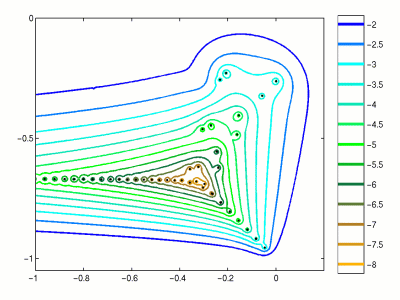
from IPython.core.display import HTML
def css_styling():
styles = open("./styles/custom.css", "r").read()
return HTML(styles)
css_styling()