- (2 pts) Run the power method for the graph presented above and plot residuals $\|Ax_k - \lambda_k x_k\|_2$ as a function of $k$ for
num_iter=100 and random initial guess x0. Explain the absence of convergence.
- (2 pts) Consider the same graph, but with additional self loop at node 4 (self loop is an edge that connects a vertex with itself). Plot residuals as in the previous task and discuss the convergence. Now, run the power method with
num_iter=100 for 10 different initial guesses and print/plot the resulting approximated eigenvectors. Why do they depend on the initial guess?
In order to avoid this problem Larry Page and Sergey Brin proposed to use the following regularization technique:
$$
A_d = dA + \frac{1-d}{N} \begin{pmatrix} 1 & \dots & 1 \\ \vdots & & \vdots \\ 1 & \dots & 1 \end{pmatrix},
$$
where $d$ is a small parameter in $[0,1]$ (typically $d=0.85$), which is called damping factor, $A$ is of size $N\times N$. Now $A_d$ is the matrix with multiplicity of the largest eigenvalue equal to 1.
Recall that computing the eigenvector of the PageRank matrix, which corresponds to the largest eigenvalue, has the following interpretation. Consider a person who stays in a random node of a graph (i.e. opens a random web page); at each step s/he follows one of the outcoming edges uniformly at random (i.e. opens one of the links). So the person randomly walks through the graph and the eigenvector we are looking for is exactly his/her stationary distribution — for each node it tells you the probability of visiting this particular node. Therefore, if the person has started from a part of the graph which is not connected with the other part, he will never get there. In the regularized model, the person at each step follows one of the outcoming links with probability $d$ OR teleports to a random node from the whole graph with probability $(1-d)$.
(2 pts) Now, run the power method with $A_d$ and plot residuals $\|A_d x_k - \lambda_k x_k\|_2$ as a function of $k$ for $d=0.97$, num_iter=100 and a random initial guess x0.
(5 pts) Find the second largest in the absolute value eigenvalue of the obtained matrix $A_d$. How and why is it connected to the damping factor $d$? What is the convergence rate of the PageRank algorithm when using damping factor?
Usually, graphs that arise in various areas are sparse (social, web, road networks, etc.) and, thus, computation of a matrix-vector product for corresponding PageRank matrix $A$ is much cheaper than $\mathcal{O}(N^2)$. However, if $A_d$ is calculated directly, it becomes dense and, therefore, $\mathcal{O}(N^2)$ cost grows prohibitively large for big $N$.
(2 pts) Implement fast matrix-vector product for $A_d$ as a function pagerank_matvec(A, d, x), which takes a PageRank matrix $A$ (in sparse format, e.g., csr_matrix), damping factor $d$ and a vector $x$ as an input and returns $A_dx$ as an output.
(1 pts) Generate a random adjacency matrix of size $10000 \times 10000$ with only 100 non-zero elements and compare pagerank_matvec performance with direct evaluation of $A_dx$.
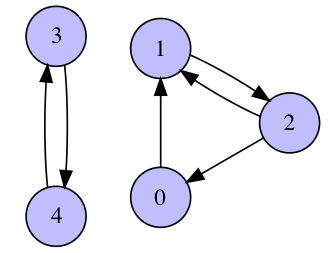 What is its largest eigenvalue? What multiplicity does it have?
What is its largest eigenvalue? What multiplicity does it have?