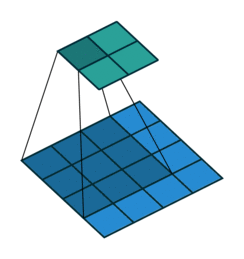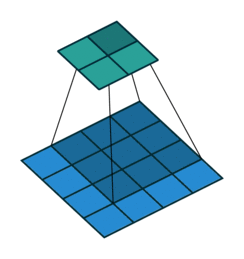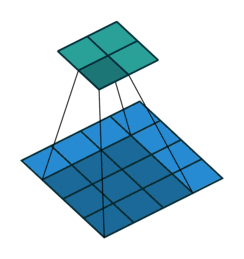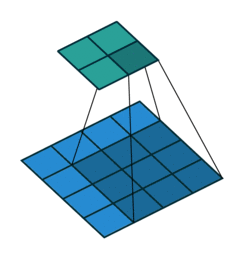
Sequential(
(0): Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace=True)
(2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(3): ReLU(inplace=True)
(4): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(5): Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(6): ReLU(inplace=True)
(7): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(8): ReLU(inplace=True)
(9): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(10): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU(inplace=True)
(12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(13): ReLU(inplace=True)
(14): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(15): ReLU(inplace=True)
(16): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(17): Conv2d(256, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(18): ReLU(inplace=True)
(19): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(20): ReLU(inplace=True)
(21): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(22): ReLU(inplace=True)
(23): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(24): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(25): ReLU(inplace=True)
(26): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(27): ReLU(inplace=True)
(28): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(29): ReLU(inplace=True)
(30): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
)
0.weight torch.Size([64, 3, 3, 3])
0.bias torch.Size([64])
2.weight torch.Size([64, 64, 3, 3])
2.bias torch.Size([64])
5.weight torch.Size([128, 64, 3, 3])
5.bias torch.Size([128])
7.weight torch.Size([128, 128, 3, 3])
7.bias torch.Size([128])
10.weight torch.Size([256, 128, 3, 3])
10.bias torch.Size([256])
12.weight torch.Size([256, 256, 3, 3])
12.bias torch.Size([256])
14.weight torch.Size([256, 256, 3, 3])
14.bias torch.Size([256])
17.weight torch.Size([512, 256, 3, 3])
17.bias torch.Size([512])
19.weight torch.Size([512, 512, 3, 3])
19.bias torch.Size([512])
21.weight torch.Size([512, 512, 3, 3])
21.bias torch.Size([512])
24.weight torch.Size([512, 512, 3, 3])
24.bias torch.Size([512])
26.weight torch.Size([512, 512, 3, 3])
26.bias torch.Size([512])
28.weight torch.Size([512, 512, 3, 3])
28.bias torch.Size([512])