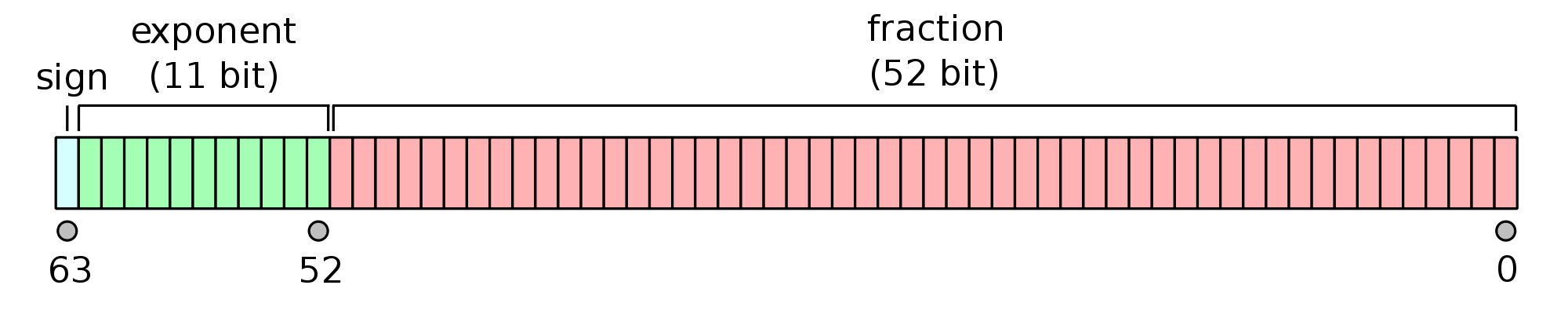
Representation of numbers¶
- Real numbers represent quantities: probabilities, velocities, masses, ...

- It is important to know, how they are represented in the computer, which only knows about bits.
Today:
Tomorrow: Matrix norms and unitary matrices

The most straightforward format for the representation of real numbers is fixed point representation, also known as Qm.n format.
A Qm.n number is in the range $[-(2^m), 2^m - 2^{-n}]$, with resolution $2^{-n}$.
Total storage is $m + n + 1$ bits.
The range of numbers represented is fixed.
The numbers in computer memory are typically represented as floating point numbers
A floating point number is represented as
$$\textrm{number} = \textrm{significand} \times \textrm{base}^{\textrm{exponent}},$$where significand is integer, base is positive integer and exponent is integer (can be negative), i.e.
$$ 1.2 = 12 \cdot 10^{-1}.$$where $s \in \{0, 1\}$ is the sign bit, $d_i \in \{0, 1\}$ is the $m$-bit mantissa, $p \in \mathbb{Z}; 0 \leq p \leq 2^e$, $e$ is the $e$-bit exponent, commonly defined as $2^e - 1$
Can be thought as a uniform $m$-bit grid between two sequential powers of $2$.
Q: What are the advantages/disadvantages of the fixed and floating points?
A: In most cases, they work just fine.
However, fixed point represents numbers within specified range and controls absolute accuracy.
Floating point represent numbers with relative accuracy, and is suitable for the case when numbers in the computations have varying scale (i.e., $10^{-1}$ and $10^{5}$).
In practice, if speed is of no concern, use float32 or float64.
In modern computers, the floating point representation is controlled by IEEE 754 standard which was published in 1985 and before that point different computers behaved differently with floating point numbers.
IEEE 754 has:
Possible values are defined with
and have the following restrictions
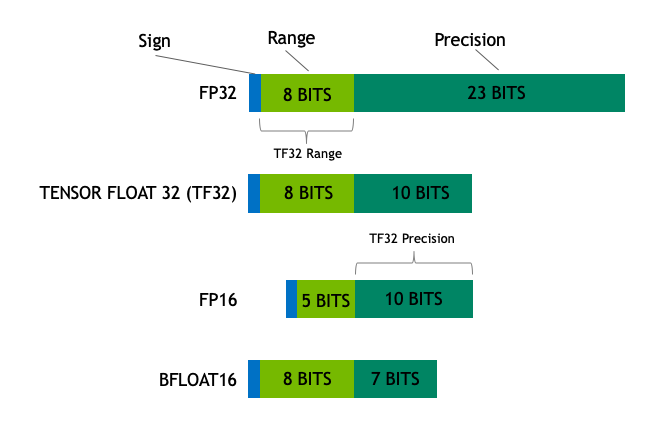
The two most common formats, called binary32 and binary64 (called also single and double formats). Recently, the format binary16 plays important role in learning deep neural networks.
| Name | Common Name | Base | Digits | Emin | Emax |
|---|---|---|---|---|---|
| binary16 | half precision | 2 | 11 | -14 | + 15 |
| binary32 | single precision | 2 | 24 | -126 | + 127 |
| binary64 | double precision | 2 | 53 | -1022 | +1023 |
Q: what about -infinity and NaN ?
The relative accuracy of single precision is $10^{-7}-10^{-8}$, while for double precision is $10^{-14}-10^{-16}$.
Crucial note 1: A float16 takes 2 bytes, float32 takes 4 bytes, float64, or double precision, takes 8 bytes.
Crucial note 2: These are the only two floating point-types supported in hardware (float32 and float64) + GPU/TPU different float types are supported.
Crucial note 3: You should use double precision in computational science and engineering and float on GPU/Data Science.
Also, half precision can be useful in training deep neural network, see this paper.
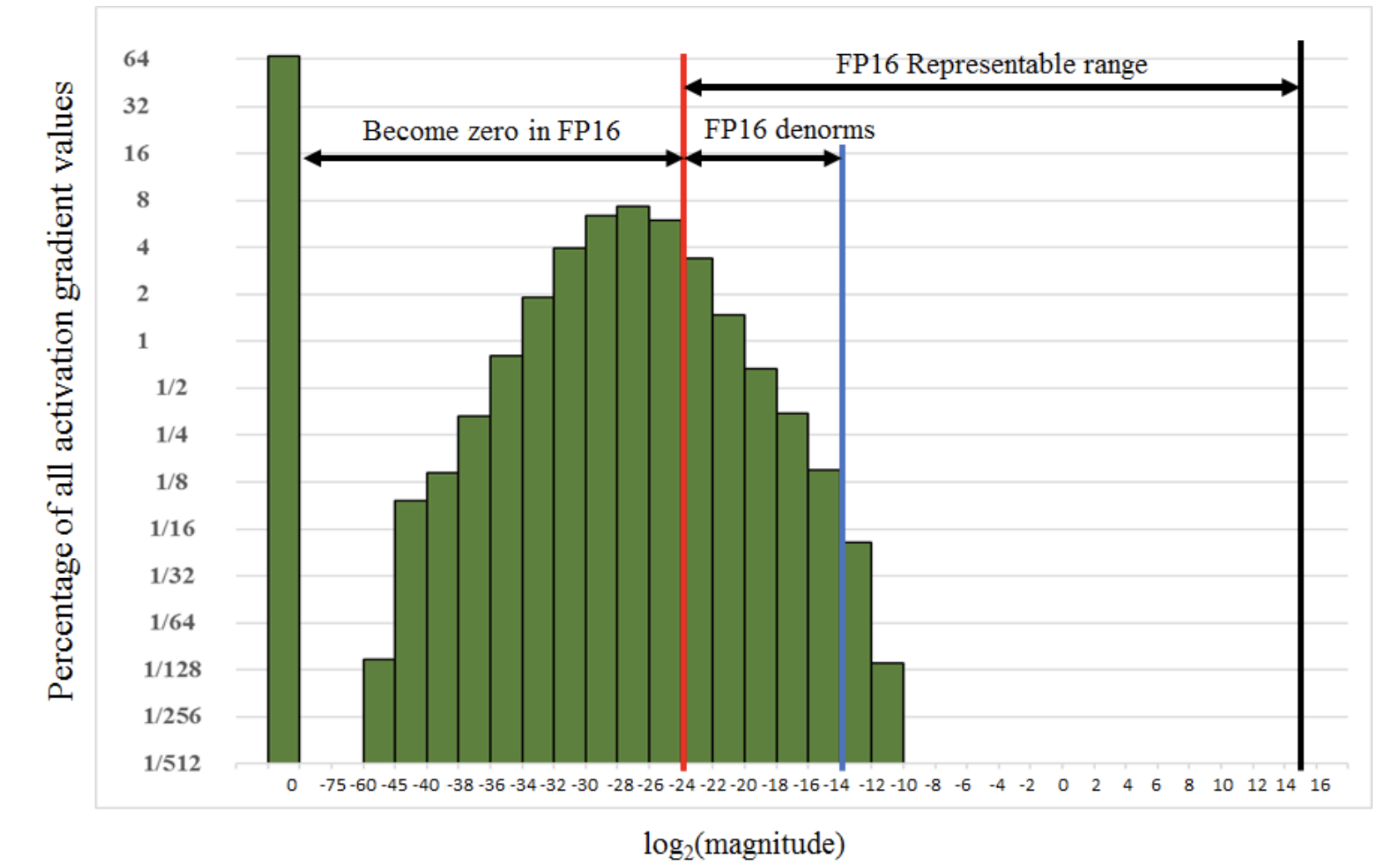
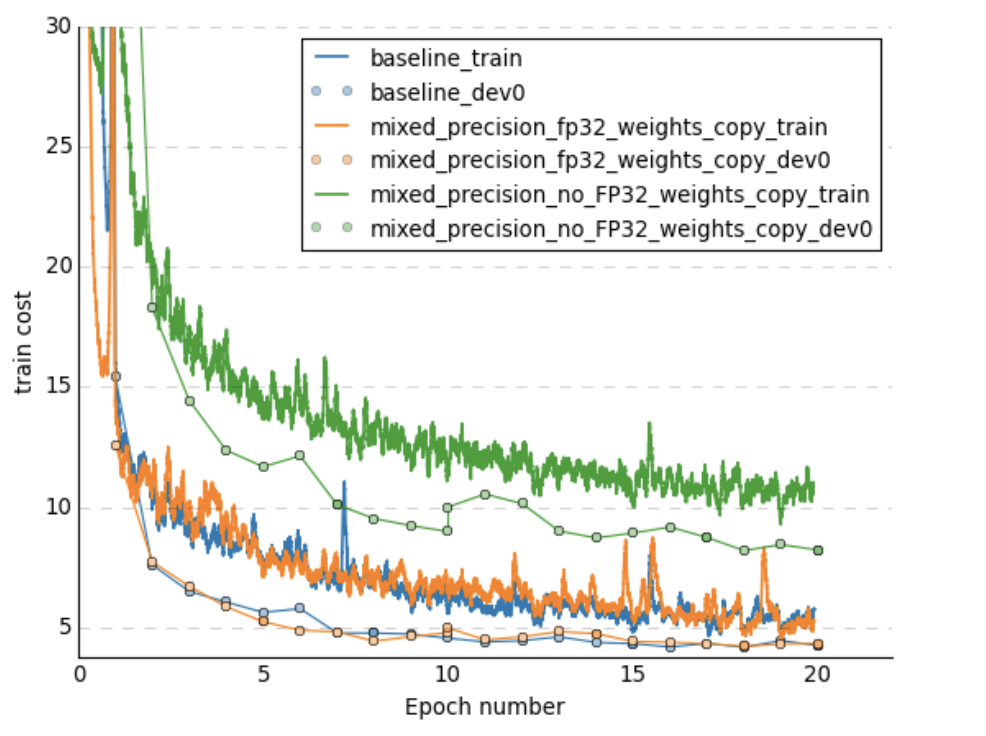
Plots are taken from this paper


Performance comparison
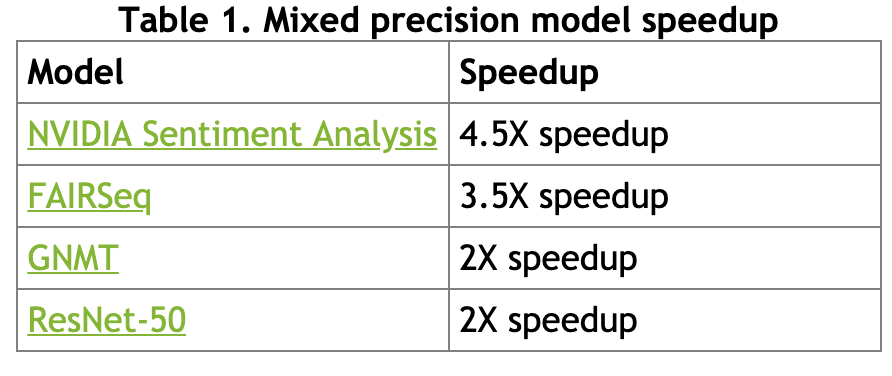
Automatic mixed-precision extensions exist to simplify turning this option on, more details here
Issues in IEEE 754:
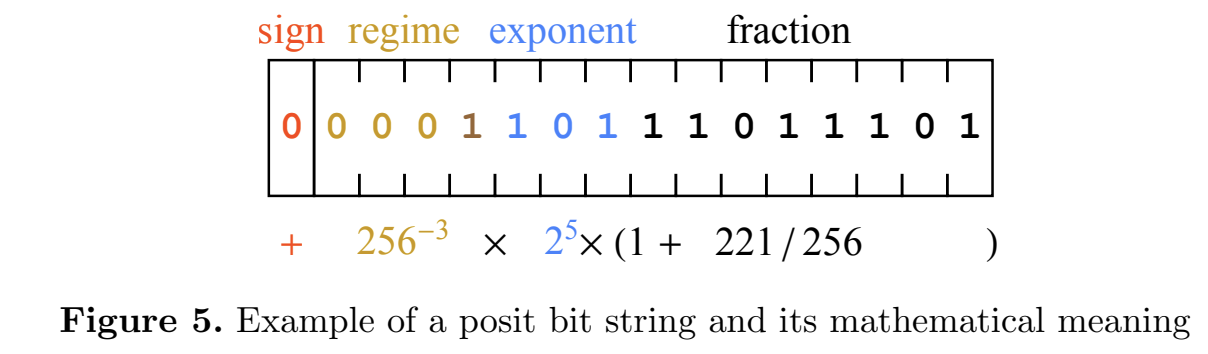
Concept of posits can replace floating point numbers, see this paper

import random
import jax.numpy as jnp
import jax
from jax.config import config
config.update("jax_enable_x64", True)
#c = random.random()
#print(c)
c = jnp.float32(0.925924589693)
print(c)
a = jnp.float32(1e-50)
b = jnp.float32(c / a)
print('{0:10.16f}'.format(b))
print(abs(a * b - c)/abs(c))
0.9259246
inf
nan
a = jnp.float32(1e-40)
b = jnp.sqrt(a)
print(b.dtype)
print('{0:10.64f}'.format(abs(b * b - a)/abs(a)))
float32
nan
a = jnp.float32(1e99)
b = jnp.exp(a)
print(b.dtype)
print(jnp.log(b) - a)
float32 nan
However, the rounding errors can depend on the algorithm.
Consider the simplest problem: given $n$ floating point numbers $x_1, \ldots, x_n$
Compute their sum
The simplest algorithm is to add one-by-one
What is the actual error for such algorithm?
Naïve algorithm adds numbers one-by-one:
$$y_1 = x_1, \quad y_2 = y_1 + x_2, \quad y_3 = y_2 + x_3, \ldots.$$The worst-case error is then proportional to $\mathcal{O}(n)$, while mean-squared error is $\mathcal{O}(\sqrt{n})$.
The Kahan algorithm gives the worst-case error bound $\mathcal{O}(1)$ (i.e., independent of $n$).
Can you find the better algorithm?
The following algorithm gives $2 \varepsilon + \mathcal{O}(n \varepsilon^2)$ error, where $\varepsilon$ is the machine precision.
s = 0
c = 0
for i in range(len(x)):
y = x[i] - c
t = s + y
c = (t - s) - y
s = t
fsum function from math package, implementation check out here import math
import jax.numpy as jnp
import numpy as np
import jax
from numba import jit as numba_jit
n = 10 ** 7
sm = 1e-10
x = jnp.ones(n, dtype=jnp.float32) * sm
x = x.at[0].set(1)
#x = jax.ops.index_update(x, [0], 1.)
true_sum = 1.0 + (n - 1)*sm
approx_sum = jnp.sum(x)
math_fsum = math.fsum(x)
@jax.jit
def dumb_sum(x):
s = jnp.float32(0.0)
def b_fun(i, val):
return val + x[i]
s = jax.lax.fori_loop(0, len(x), b_fun, s)
return s
@numba_jit(nopython=True)
def kahan_sum_numba(x):
s = np.float32(0.0)
c = np.float32(0.0)
for i in range(len(x)):
y = x[i] - c
t = s + y
c = (t - s) - y
s = t
return s
@jax.jit
def kahan_sum_jax(x):
s = jnp.float32(0.0)
c = jnp.float32(0.0)
def b_fun2(i, val):
s, c = val
y = x[i] - c
t = s + y
c = (t - s) - y
s = t
return s, c
s, c = jax.lax.fori_loop(0, len(x), b_fun2, (s, c))
return s
k_sum_numba = kahan_sum_numba(np.array(x))
k_sum_jax = kahan_sum_jax(x)
d_sum = dumb_sum(x)
print('Error in np sum: {0:3.1e}'.format(approx_sum - true_sum))
print('Error in Kahan sum Numba: {0:3.1e}'.format(k_sum_numba - true_sum))
print('Error in Kahan sum JAX: {0:3.1e}'.format(k_sum_jax - true_sum))
print('Error in dumb sum: {0:3.1e}'.format(d_sum - true_sum))
print('Error in math fsum: {0:3.1e}'.format(math_fsum - true_sum))
Error in np sum: -8.3e-07 Error in Kahan sum Numba: 4.7e-08 Error in Kahan sum JAX: 0.0e+00 Error in dumb sum: -1.0e-03 Error in math fsum: 1.3e-11
import math
test_list = [1, 1e20, 1, -1e20]
print(math.fsum(test_list))
print(jnp.sum(jnp.array(test_list, dtype=jnp.float32)))
print(1 + 1e20 + 1 - 1e20)
2.0 0.0 0.0
You should be really careful with floating point numbers, since it may give you incorrect answers due to rounding-off errors.
For many standard algorithms, the stability is well-understood and problems can be easily detected.
Example: Polynomials with degree $\leq n$ form a linear space. Polynomial $ x^3 - 2x^2 + 1$ can be considered as a vector $\begin{bmatrix}1 \\ -2 \\ 0 \\ 1\end{bmatrix}$ in the basis $\{x^3, x^2, x, 1\}$
Vectors typically provide an (approximate) description of a physical (or some other) object
One of the main question is how accurate the approximation is (1%, 10%)
What is an acceptable representation, of course, depends on the particular applications. For example:
The norm should satisfy certain properties:
The distance between two vectors is then defined as
$$ d(x, y) = \Vert x - y \Vert. $$The most well-known and widely used norm is euclidean norm:
$$\Vert x \Vert_2 = \sqrt{\sum_{i=1}^n |x_i|^2},$$which corresponds to the distance in our real life. If the vectors have complex elements, we use their modulus.
Euclidean norm, or $2$-norm, is a subclass of an important class of $p$-norms:
$$ \Vert x \Vert_p = \Big(\sum_{i=1}^n |x_i|^p\Big)^{1/p}. $$There are two very important special cases:

We will give examples where $L_1$ norm is very important: it all relates to the compressed sensing methods that emerged in the mid-00s as one of the most popular research topics.
All norms are equivalent in the sense that
$$ C_1 \Vert x \Vert_* \leq \Vert x \Vert_{**} \leq C_2 \Vert x \Vert_* $$for some positive constants $C_1(n), C_2(n)$, $x \in \mathbb{R}^n$ for any pairs of norms $\Vert \cdot \Vert_*$ and $\Vert \cdot \Vert_{**}$. The equivalence of the norms basically means that if the vector is small in one norm, it is small in another norm. However, the constants can be large.
The NumPy package has all you need for computing norms: np.linalg.norm function.
n = 100
a = jnp.ones(n)
b = a + 1e-3 * jax.random.normal(jax.random.PRNGKey(0), (n,))
print('Relative error in L1 norm:', jnp.linalg.norm(a - b, 1) / jnp.linalg.norm(b, 1))
print('Relative error in L2 norm:', jnp.linalg.norm(a - b) / jnp.linalg.norm(b))
print('Relative error in Chebyshev norm:', jnp.linalg.norm(a - b, jnp.inf) / jnp.linalg.norm(b, jnp.inf))
Relative error in L1 norm: 0.0008608277121789923 Relative error in L2 norm: 0.0010668749128008221 Relative error in Chebyshev norm: 0.0025285461541625647
%matplotlib inline
import matplotlib.pyplot as plt
p = 0.5 # Which norm do we use
M = 4000 # Number of sampling points
b = []
for i in range(M):
a = jax.random.normal(jax.random.PRNGKey(i), (1, 2))
if jnp.linalg.norm(a[i, :], p) <= 1:
b.append(a[i, :])
b = jnp.array(b)
plt.plot(b[:, 0], b[:, 1], '.')
plt.axis('equal')
plt.title('Unit disk in the p-th norm, $p={0:}$'.format(p))
Text(0.5, 1.0, 'Unit disk in the p-th norm, $p=0.5$')
$L_1$ norm, as it was discovered quite recently, plays an important role in compressed sensing.
The simplest formulation of the considered problem is as follows:
The question: can we find the solution?
The solution is obviously non-unique, so a natural approach is to find the solution that is minimal in the certain sense:
\begin{align*} & \Vert x \Vert \rightarrow \min_x \\ \mbox{subject to } & Ax = f \end{align*}Typical choice of $\Vert x \Vert = \Vert x \Vert_2$ leads to the linear least squares problem (and has been used for ages).
The choice $\Vert x \Vert = \Vert x \Vert_1$ leads to the compressed sensing
And we finalize the lecture by the concept of stability.
You also have a numerical algorithm alg(x) that actually computes approximation to $f(x)$.
The algorithm is called forward stable, if $$\Vert \text{alg}(x) - f(x) \Vert \leq \varepsilon $$
The algorithm is called backward stable, if for any $x$ there is a close vector $x + \delta x$ such that
$$\text{alg}(x) = f(x + \delta x)$$and $\Vert \delta x \Vert$ is small.
A classical example is the solution of linear systems of equations using Gaussian elimination which is similar to LU factorization (more details later)
We consider the Hilbert matrix with the elements
$$A = \{a_{ij}\}, \quad a_{ij} = \frac{1}{i + j + 1}, \quad i,j = 0, \ldots, n-1.$$And consider a linear system
$$Ax = f.$$We will look into matrices in more details in the next lecture, and for linear systems in the upcoming weeks
import numpy as np
n = 20
a = [[1.0/(i + j + 1) for i in range(n)] for j in range(n)] # Hilbert matrix
A = jnp.array(a)
#rhs = jax.random.normal(jax.random.PRNGKey(0), (n,))
rhs = jnp.ones(n)
sol = jnp.linalg.solve(A, rhs)
print(jnp.linalg.norm(A @ sol - rhs)/jnp.linalg.norm(rhs))
plt.plot(sol)
1.2877871109130684e-08
[<matplotlib.lines.Line2D at 0x2f927eeb0>]
rhs = jnp.ones(n)
sol = jnp.linalg.solve(A, rhs)
print(jnp.linalg.norm(A @ sol - rhs)/jnp.linalg.norm(rhs))
#plt.plot(sol)
How to compute the following functions in numerically stable manner?
u = 300
eps = 1e-6
print("Original function:", jnp.log(1 - jnp.tanh(u)**2))
eps_add = jnp.log(1 - jnp.tanh(u)**2 + eps)
print("Attempt to improve stability by adding a small constant:", eps_add)
print("Use more numerically stable form:", jnp.log(4) - 2 * jnp.log(jnp.exp(-u) + jnp.exp(u)))
n = 5
x = jax.random.normal(jax.random.PRNGKey(0), (n, ))
x = jax.ops.index_update(x, [0], 1000)
print(jnp.exp(x) / jnp.sum(jnp.exp(x)))
print(jnp.exp(x - jnp.max(x)) / jnp.sum(jnp.exp(x - jnp.max(x))))