Lecture 2. Matrix norms and unitary matrices

Recap of the previous lecture

• Floating point (double, single, half precisions, number of bytes), rounding error
• Vector norms are measures of smallness, used to compute the distance and accuracy
• Forward/backward error (and stability of algorithms)

Notations

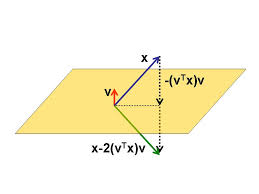
We use notation

$$A= \begin{bmatrix} a_{11} & \dots & a_{1m} \\ \vdots & \ddots & \vdots \\ a_{n1} & \dots & a_{nm} \end{bmatrix} \equiv \{a_{ij}\}_{i,j=1}^{n,m}\in \mathbb{C}^{n\times m}.$$

$A^*\stackrel{\mathrm{def}}{=}\overline{A^\top}$.

Matrices and norms

• Recall vector norms that allow to evaluate distance between two vectors or how large are elements of a vector.

• How to generalize this concept to matrices?

• A trivial answer is that there is no big difference between matrices and vectors, and here comes the simplest matrix norm –– Frobenius norm:

$$ \Vert A \Vert_F \stackrel{\mathrm{def}}{=} \Big(\sum_{i=1}^n \sum_{j=1}^m |a_{ij}|^2\Big)^{1/2} $$

Matrix norms

$\Vert \cdot \Vert$ is called a matrix norm if it is a vector norm on the vector space of $n \times m$ matrices:

1. $\|A\| \geq 0$ and if $\|A\| = 0$ then $A = O$
2. $\|\alpha A\| = |\alpha| \|A\|$
3. $\|A+B\| \leq \|A\| + \|B\|$ (triangle inequality)

Additionally some norms can satisfy the submultiplicative property

• $\Vert A B \Vert \leq \Vert A \Vert \Vert B \Vert$

• These norms are called submultiplicative norms.

• The submultiplicative property is needed in many places, for example in the estimates for the error of solution of linear systems (we will cover this topic later).

• Example of a non-submultiplicative norm is Chebyshev norm

$$ \|A\|_C = \displaystyle{\max_{i,j}}\, |a_{ij}| $$

Operator norms

• The most important class of the matrix norms is the class of operator norms. They are defined as

$$ \Vert A \Vert_{*,**} = \sup_{x \ne 0} \frac{\Vert A x \Vert_*}{\Vert x \Vert_{**}}, $$

where $\Vert \cdot \Vert_*$ and $\| \cdot \|_{**}$ are vector norms.

• It is easy to check that operator norms are submultiplicative if $\|\cdot\|_* = \|\cdot\|_{**}$. Otherwise, it can be non-submultiplicative, think about example.

• Frobenius norm is a matrix norm, but not an operator norm, i.e. you can not find $\Vert \cdot \Vert_*$ and $\| \cdot \|_{**}$ that induce it.

• This is a nontrivial fact and the general criterion for matrix norm to be an operator norm can be found in Theorem 6 and Corollary 4. For $\Vert \cdot \Vert_* = \| \cdot \|_{**}$ let us check on the blackboard!

Matrix $p$-norms

Important case of operator norms are matrix $p$-norms, which are defined for $\|\cdot\|_* = \|\cdot\|_{**} = \|\cdot\|_p$.

Among all $p$-norms three norms are the most common ones:

• $p = 1, \quad \Vert A \Vert_{1} = \displaystyle{\max_j \sum_{i=1}^n} |a_{ij}|$.

• $p = 2, \quad$ spectral norm, denoted by $\Vert A \Vert_2$.

• $p = \infty, \quad \Vert A \Vert_{\infty} = \displaystyle{\max_i \sum_{j=1}^m} |a_{ij}|$.

Let us check it for $p=\infty$ on a blackboard.

Spectral norm

• Spectral norm, $\Vert A \Vert_2$ is one of the most used matrix norms (along with the Frobenius norm).
• It can not be computed directly from the entries using a simple formula, like the Frobenius norm, however, there are efficient algorithms to compute it.
• It is directly related to the singular value decomposition (SVD) of the matrix. It holds

$$ \Vert A \Vert_2 = \sigma_1(A) = \sqrt{\lambda_\max(A^*A)} $$

where $\sigma_1(A)$ is the largest singular value of the matrix $A$ and $^*$ is a conjugate transpose of the matrix.

• We will soon learn all about the SVD. Meanwhile, we can already compute the norm in Python.

import jax.numpy as jnp
import jax
n = 100
m = 2000
a = jax.random.normal(jax.random.PRNGKey(0), (n, m)) #Random n x m matrix
s1 = jnp.linalg.norm(a, 2) #Spectral
s2 = jnp.linalg.norm(a, 'fro') #Frobenius
s3 = jnp.linalg.norm(a, 1) #1-norm
s4 = jnp.linalg.norm(a, jnp.inf) 
print('Spectral: {0:} \nFrobenius: {1:} \n1-norm: {2:} \ninfinity: {3:}'.format(s1, s2, s3, s4))

Examples

Several examples of optimization problems where matrix norms arise:

• $\displaystyle{\min_{\mathrm{rank}(A_r)=r}}\| A - A_r\|$ –– finding best rank-r approximation. SVD helps to solve this problem for $\|\cdot\|_2$ and $\|\cdot\|_F$.

• $\displaystyle{\min_B}\| P_\Omega \odot(A - B)\| + \mathrm{rank}(B)$ –– matrix completion.

$$ (P_\Omega)_{ij} = \begin{cases} 1 & i,j\in\Omega \\ 0 & \text{otherwise}, \end{cases} $$

where $\odot$ denotes Hadamard product (elementwise)

• $\displaystyle{\min_{B,C\geq 0}} \|A - BC\|_F$ –– nonnegative matrix factorization. Symbol $B\geq0$ here means that all elements of $B$ are nonnegative.

Scalar product

While norm is a measure of distance, the scalar product takes angle into account.

It is defined as

• For vectors: $$ (x, y) = x^* y = \sum_{i=1}^n \overline{x}_i y_i, $$ where $\overline{x}$ denotes the complex conjugate of $x$. The Euclidean norm is then

$$ \Vert x \Vert_2 = \sqrt{(x, x)}, $$

or it is said the norm is induced by the scalar product.

• For matrices (Frobenius scalar product):

$$ (A, B)_F = \displaystyle{\sum_{i=1}^{n}\sum_{j=1}^{m}} \overline{a}_{ij} b_{ij} \equiv \mathrm{trace}(A^* B), $$

where $\mathrm{trace}(A)$ denotes the sum of diagonal elements of $A$. One can check that $\|A\|_F = \sqrt{(A, A)_F}$.

Remark. The angle between two vectors is defined as

$$ \cos \phi = \frac{(x, y)}{\Vert x \Vert_2 \Vert y \Vert_2}. $$

Similar expression holds for matrices.

• An important property of the scalar product is the Cauchy-Schwarz-Bunyakovski inequality:

$$|(x, y)| \leq \Vert x \Vert_2 \Vert y \Vert_2,$$

and thus the angle between two vectors is defined properly.

Matrices preserving the norm

• For stability it is really important that the error does not grow after we apply some transformations.

• Suppose you are given $\widehat{x}$ –– the approximation of $x$ such that,

$$ \frac{\Vert x - \widehat{x} \Vert}{\Vert x \Vert} \leq \varepsilon. $$

• Let us calculate a linear transformation of $x$ and $\widehat{x}$:

$$ y = U x, \quad \widehat{y} = U \widehat{x}. $$

• When building new algorithms, we want to use transformations that do not increase (or even preserve) the error:

$$ \frac{\Vert y - \widehat{y} \Vert}{\Vert y \Vert } = \frac{\Vert U ( x - \widehat{x}) \Vert}{\Vert U x\Vert} \leq \varepsilon. $$

• The question is for which kind of matrices the norm of the vector will not change, so that

$$ \frac{\Vert U ( x - \widehat{x}) \Vert}{\Vert U x\Vert} = \frac{ \|x - \widehat{x}\|}{\|x\|}. $$

• For the euclidean norm $\|\cdot\|_2$ the answer is unitary (or orthogonal in the real case) matrices.

Unitary (orthogonal) matrices

• Let $U$ be complex $n \times n$ matrix, and $\Vert U z \Vert_2 = \Vert z \Vert_2$ for all $z$.

• This can happen if and only if (can be abbreviated as iff)

$$ U^* U = I_n, $$

where $I_n$ is an identity matrix $n\times n$.

• Complex $n\times n$ square matrix is called unitary if

$$ U^*U = UU^* = I_n, $$

which means that columns and rows of unitary matrices both form orthonormal basis in $\mathbb{C}^{n}$.

• For rectangular matrices of size $m\times n$ ($n\not= m$) only one of the equalities can hold

  • $ U^*U = I_n$ –– left unitary for $m>n$
  • $ UU^* = I_m$ –– right unitary for $m<n$

• In the case of real matrices $U^* = U^T$ and matrices such that

$$ U^TU = UU^T = I $$

are called orthogonal.

Unitary matrices

Important property: a product of two unitary matrices is a unitary matrix:

$$(UV)^* UV = V^* (U^* U) V = V^* V = I,$$

• Later we will show that there are types of matrices (Householder reflections and Givens rotations) composition of which is able to produce arbitrary unitary matrix
• This idea is a core of some algorithms, e.g. QR decomposition

Unitary invariance of $\|\cdot\|_2$ and $\|\cdot\|_F$ norms

• For vector 2-norm we have already seen that $\Vert U z \Vert_2 = \Vert z \Vert_2$ for any unitary $U$.

• One can show that unitary matrices also do not change matrix norms $\|\cdot\|_2$ and $\|\cdot\|_F$, i.e. for any square $A$ and unitary $U$,$V$:

$$ \| UAV\|_2 = \| A \|_2 \qquad \| UAV\|_F = \| A \|_F.$$

• For $\|\cdot\|_2$ it follows from the definition of an operator norm and the fact that vector 2-norm is unitary invariant.

• For $\|\cdot\|_F$ it follows from $\|A\|_F^2 = \mathrm{trace}(A^*A)$ and the fact that $\mathrm{trace}(BC) = \mathrm{trace}(CB)$.

Examples of unitary matrices

• There are two important classes of unitary matrices, using composition of which we can construct any unitary matrix:

  1. Householder matrices
  2. Givens (Jacobi) matrices

• Other important examples are

  • Permutation matrix $P$ whose rows (columns) are permutation of rows (columns) of the identity matrix.
  • Fourier matrix $F_n = \frac{1}{\sqrt{n}} \left\{ e^{-i\frac{2\pi kl}{n}}\right\}_{k,l=0}^{n-1}$

Householder matrices

• Householder matrix is the matrix of the form

$$H \equiv H(v) = I - 2 vv^*,$$

where $v$ is an $n \times 1$ column and $v^* v = 1$.

• Can you show that $H$ is unitary and Hermitian ($H^* = H$)?
• It is also a reflection:

$$ Hx = x - 2(v^* x) v$$

Important property of Householder reflection

• A nice property of Householder transformation is that it can zero all elements of a vector except for the first one:

$$ H \begin{bmatrix} \times \\ \times \\ \times \\ \times \end{bmatrix} = \begin{bmatrix} \times \\ 0 \\ 0 \\ 0 \end{bmatrix}. $$

Proof (for real case). Let $e_1 = (1,0,\dots, 0)^T$, then we want to find $v$ such that

$$ H x = x - 2(v^* x) v = \alpha e_1, $$

where $\alpha$ is an unknown constant. Since $\|\cdot\|_2$ is unitary invariant we get

$$\|x\|_2 = \|Hx\|_2 = \|\alpha e_1\|_2 = |\alpha|.$$

and $$\alpha = \pm \|x\|_2$$

Also, we can express $v$ from $x - 2(v^* x) v = \alpha e_1$:

$$v = \dfrac{x-\alpha e_1}{2 v^* x}$$

Multiplying the latter expression by $x^*$ we get

$$x^* x - 2 (v^* x) x^* v = \alpha x_1; $$

or

$$ \|x\|_2^2 - 2 (v^* x)^2 = \alpha x_1. $$

Therefore,

$$ (v^* x)^2 = \frac{\|x\|_2^2 - \alpha x_1}{2}. $$

So, $v$ exists and equals

$$ v = \dfrac{x \mp \|x\|_2 e_1}{2v^* x} = \dfrac{x \mp \|x\|_2 e_1}{\pm\sqrt{2(\|x\|_2^2 \mp \|x\|_2 x_1)}}. $$

Householder algorithm for QR decomposition

Using the obtained property we can make arbitrary matrix $A$ lower triangular:

$$ H_2 H_1 A = \begin{bmatrix} \times & \times & \times & \times \\ 0 & \times & \times & \times \\ 0 & 0 & \boldsymbol{\times} & \times\\ 0 &0 & \boldsymbol{\times} & \times \\ 0 &0 & \boldsymbol{\times} & \times \end{bmatrix} $$

then finding $H_3=\begin{bmatrix}I_2 & \\ & {\widetilde H}_3 \end{bmatrix}$ such that

$$ {\widetilde H}_3 \begin{bmatrix} \boldsymbol{\times}\\ \boldsymbol{\times} \\ \boldsymbol{\times} \end{bmatrix} = \begin{bmatrix} \times \\ 0 \\ 0 \end{bmatrix}. $$

we get

$$ H_3 H_2 H_1 A = \begin{bmatrix} \times & \times & \times & \times \\ 0 & \times & \times & \times \\ 0 & 0 & {\times} & \times\\ 0 &0 & 0 & \times \\ 0 &0 & 0 & \times \end{bmatrix} $$

Finding $H_4$ by analogy we arrive at upper-triangular matrix.

Since product and inverse of unitary matrices is a unitary matrix we get:

Corollary: (QR decomposition) Every $A\in \mathbb{C}^{n\times m}$ can be represented as

$$ A = QR, $$

where $Q$ is unitary and $R$ is upper triangular.

See poster, what are the sizes of $Q$ and $R$ for $n>m$ and $n<m$.

Givens (Jacobi) matrix

• A Givens matrix is a matrix

$$ G = \begin{bmatrix} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{bmatrix},$$

which is a rotation.

• For a general case, we select two $(i, j)$ planes and rotate vector $x$

$$ x' = G x, $$

only in the $i$-th and $j$-th positions:

$$ x'_i = x_i\cos \alpha - x_j\sin \alpha , \quad x'_j = x_i \sin \alpha + x_j\cos\alpha, $$

with all other $x_i$ remain unchanged.

• Therefore, we can make elements in the $j$-th position zero by choosing $\alpha$ such that

$$ \cos \alpha = \frac{x_i}{\sqrt{x_i^2 + x_j^2}}, \quad \sin \alpha = -\frac{x_j}{\sqrt{x_i^2 + x_j^2}} $$

import jax.numpy as jnp
import matplotlib.pyplot as plt
%matplotlib inline

alpha = -3*jnp.pi / 4
G = jnp.array([
    [jnp.cos(alpha), -jnp.sin(alpha)],
    [jnp.sin(alpha), jnp.cos(alpha)]
])
x = jnp.array([-1./jnp.sqrt(2), 1./jnp.sqrt(2)])
y = G @ x

plt.quiver([0, 0], [0, 0], [x[0], y[0]], [x[1], y[1]], angles='xy', scale_units='xy', scale=1)
plt.xlim(-1., 1.)
plt.ylim(-1., 1.)

QR via Givens rotations

Similarly we can make matrix upper-triangular using Givens rotations:

$$\begin{bmatrix} \times & \times & \times \\ \bf{*} & \times & \times \\ \bf{*} & \times & \times \end{bmatrix} \to \begin{bmatrix} * & \times & \times \\ * & \times & \times \\ 0 & \times & \times \end{bmatrix} \to \begin{bmatrix} \times & \times & \times \\ 0 & * & \times \\ 0 & * & \times \end{bmatrix} \to \begin{bmatrix} \times & \times & \times \\ 0 & \times & \times \\ 0 & 0 & \times \end{bmatrix} $$

Givens vs. Householder transformations

• Householder reflections are useful for dense matrices (complexity is $\approx$ twice smaller than for Jacobi) and we need to zero large number of elements.
• Givens rotations are more suitable for sparse matrice or parallel machines as they act locally on elements.

Singular Value Decomposition

SVD will be considered later in more details.

Theorem. Any matrix $A\in \mathbb{C}^{n\times m}$ can be written as a product of three matrices:

$$ A = U \Sigma V^*, $$

where

• $U$ is an $n \times n$ unitary matrix
• $V$ is an $m \times m$ unitary matrix
• $\Sigma$ is a diagonal matrix with non-negative elements $\sigma_1 \geq \ldots, \geq \sigma_{\min (m,n)}$ on the diagonal.

Moreover, if $\text{rank}(A) = r$, then $\sigma_{r+1} = \dots = \sigma_{\min (m,n)} = 0$.

See poster for the visualization.

• Important note: if one truncates (replace by $0$) all singular values except for $r$ first, then the resulting matrix yields best rank-$r$ approximation both in $\|\cdot\|_2$ and $\|\cdot\|_F$.
• This is called Eckart-Young theorem and will be proved later in our course.

Summary

• Most important matrix norms: Frobenius and spectral

• Unitary matrices preserve these norms

• There are two "basic" classes of unitary matrices: Householder and Givens matrices

Questions?

from IPython.core.display import HTML
def css_styling():
    styles = open("../styles/custom.css", "r").read()
    return HTML(styles)
css_styling()