Flops –– floating point operations per second.
Giga = $2^{30} \approx 10^9$,
Tera = $2^{40} \approx 10^{12}$,
Peta = $2^{50} \approx 10^{15}$,
Exa = $2^{60} \approx 10^{18}$
What is the peak perfomance of:
FLOPS = sockets (cores per socket) (number of clock cycles per second) * (number of floating point operations per cycle).
Multiplication of an $n\times n$ matrix $A$ by a vector $x$ of size $n\times 1$ ($y=Ax$):
$$ y_{i} = \sum_{i=1}^n a_{ij} x_j $$requires $n^2$ mutliplications and $n(n-1)$ additions. Thus, the overall complexity is $2n^2 - n =$ $\mathcal{O}(n^2)$
Let $A$ be the matrix of pairwise gravitational interaction between planets in a galaxy.
The number of planets in an average galaxy is $10^{11}$, so the size of this matrix is $10^{11} \times 10^{11}$.
To model evolution in time we have to multiply this matrix by vector at each time step.
Top supercomputers do around $10^{16}$ floating point operations per second (flops), so the time required to multiply the matrix $A$ by a vector is approximately
for one time step. If we could multiply it with $\mathcal{O}(n)$ complexity, we would get
\begin{align*} \frac{10^{11} \text{ operations}}{10^{16} \text{ flops}} = 10^{-5} \text{ sec}. \end{align*}Here is the YouTube video that illustrates collision of two galaxisies which was modelled by $\mathcal{O}(n \log n)$ algorithm:
from IPython.display import YouTubeVideo
YouTubeVideo("7HF5Oy8IMoM")
Fortunately, we can be faster for certain types of matrices. Here are some examples:
The simplest example may be a matrix of all ones, which can be easily multiplied with only $n-1$ additions. This matrix is of rank one. More generally we can multiply fast by low-rank matrices (or by matrices that have low-rank blocks)
Sparse matrices (contain $\mathcal{O}(n)$ nonzero elements)
Structured matrices:
Consider composition of two linear operators:
Then, $z = Ay = A B x = C x$, where $C$ is the matrix-by-matrix product.
Definition. A product of an $n \times k$ matrix $A$ and a $k \times m$ matrix $B$ is a $n \times m$ matrix $C$ with the elements
$$
c_{ij} = \sum_{s=1}^k a_{is} b_{sj}, \quad i = 1, \ldots, n, \quad j = 1, \ldots, m
$$
For $m=k=n$ complexity of a naïve algorithm is $2n^3 - n^2 =$ $\mathcal{O}(n^3)$.
Matrix-by-matrix product is the core for almost all efficient algorithms in numerical linear algebra.
Basically, all the dense NLA algorithms are reduced to a sequence of matrix-by-matrix products.
Efficient implementation of MM reduces the complexity of numerical algorithms by the same factor.
However, implementing MM is not easy at all!
Q1: Is it easy to multiply a matrix by a matrix in the most efficient way?
If you want it as fast as possible, using the computers that are at hand.
Let us do a short demo and compare a np.dot() procedure which in my case uses MKL with a hand-written matrix-by-matrix routine in Python and also its numba version.
import numpy as np
def matmul(a, b):
n = a.shape[0]
k = a.shape[1]
m = b.shape[1]
c = np.zeros((n, m))
for i in range(n):
for j in range(m):
for s in range(k):
c[i, j] += a[i, s] * b[s, j]
return c
import numpy as np
from numba import jit # Just-in-time compiler for Python, see http://numba.pydata.org
@jit(nopython=True)
def numba_matmul(a, b):
n = a.shape[0]
k = a.shape[1]
m = b.shape[1]
c = np.zeros((n, m))
for i in range(n):
for j in range(m):
for s in range(k):
c[i, j] += a[i, s] * b[s, j]
return c
Then we just compare computational times.
Guess the answer.
import jax.numpy as jnp
from jax.config import config
config.update("jax_enable_x64", True)
n = 100
a = np.random.randn(n, n)
b = np.random.randn(n, n)
a_jax = jnp.array(a)
b_jax = jnp.array(b)
%timeit matmul(a, b)
%timeit numba_matmul(a, b)
%timeit a @ b
%timeit (a_jax @ b_jax).block_until_ready()
266 ms ± 2.64 ms per loop (mean ± std. dev. of 7 runs, 1 loop each) 711 µs ± 14 µs per loop (mean ± std. dev. of 7 runs, 1 loop each) 101 µs ± 17.5 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each) 63.6 µs ± 13.8 µs per loop (mean ± std. dev. of 7 runs, 1 loop each)
Is this answer correct for any dimensions of matrices?
import matplotlib.pyplot as plt
%matplotlib inline
dim_range = [10*i for i in range(1, 11)]
time_range_matmul = []
time_range_numba_matmul = []
time_range_np = []
for n in dim_range:
print("Dimension = {}".format(n))
a = np.random.randn(n, n)
b = np.random.randn(n, n)
t = %timeit -o -q matmul(a, b)
time_range_matmul.append(t.best)
t = %timeit -o -q numba_matmul(a, b)
time_range_numba_matmul.append(t.best)
t = %timeit -o -q np.dot(a, b)
time_range_np.append(t.best)
Dimension = 10 Dimension = 20 Dimension = 30 Dimension = 40 Dimension = 50 Dimension = 60 Dimension = 70 Dimension = 80 Dimension = 90 Dimension = 100
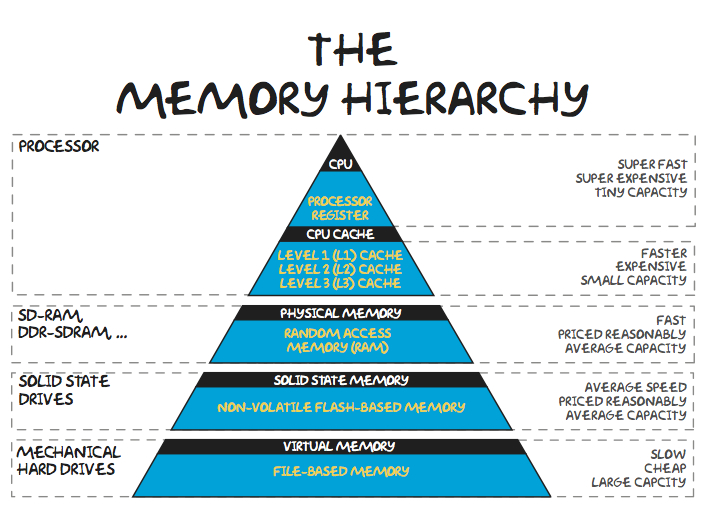
plt.plot(dim_range, time_range_matmul, label="Matmul")
plt.plot(dim_range, time_range_numba_matmul, label="Matmul Numba")
plt.plot(dim_range, time_range_np, label="Numpy")
plt.legend(fontsize=18)
plt.xlabel("Dimension", fontsize=18)
plt.ylabel("Time", fontsize=18)
plt.yscale("log")
It is slow due to two issues:
**Implementation in NLA**: use block version of algorithms.
This approach is a core of BLAS (Basic Linear Algebra Subroutines), written in Fortran many years ago, and still rules the computational world.
Split the matrix into blocks! For illustration consider splitting in $2 \times 2$ block matrix:
$$ A = \begin{bmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{bmatrix}, \quad B = \begin{bmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{bmatrix}$$Then,
$$AB = \begin{bmatrix}A_{11} B_{11} + A_{12} B_{21} & A_{11} B_{12} + A_{12} B_{22} \\ A_{21} B_{11} + A_{22} B_{21} & A_{21} B_{12} + A_{22} B_{22}\end{bmatrix}.$$If $A_{11}, B_{11}$ and their product fit into the cache memory (which is 20 Mb (L3) for the recent Intel Chip)), then we load them only once into the memory.
BLAS has three levels:
What is the principal differences between them?
The main difference is the number of operations vs. the number of input data!
Intel MKL - Math Kernel Library. It provides re-implementation of BLAS and LAPACK, optimized for Intel processors. Available in Anaconda Python distribution:
conda install mklMATLAB uses Intel MKL by default.
OpenBLAS is an optimized BLAS library based on GotoBLAS.
PyTorch supports some calls from BLAS and LAPACK
For GPU it was implemented special cuBLAS.
For comparison of OpenBLAS and Intel MKL, see this review
Recall that matrix-matrix multiplication costs $\mathcal{O}(n^3)$ operations. However, storage is $\mathcal{O}(n^2)$.
Question: is it possible to reduce number operations down to $\mathcal{O}(n^2)$?
Answer: a quest for $\mathcal{O}(n^2)$ matrix-by-matrix multiplication algorithm is not yet done.
Strassen gives $\mathcal{O}(n^{2.807\dots})$ –– sometimes used in practice
Current world record $\mathcal{O}(n^{2.37\dots})$ –– big constant, not practical, based on Coppersmith-Winograd_algorithm.
Consider Strassen in more details.
Let $A$ and $B$ be two $2\times 2$ matrices. Naïve multiplication $C = AB$
$$ \begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{21} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{21} + a_{22}b_{22} \end{bmatrix} $$contains $8$ multiplications and $4$ additions.
In the work Gaussian elimination is not optimal (1969) Strassen found that one can calculate $C$ using 18 additions and only 7 multiplications: $$ \begin{split} c_{11} &= f_1 + f_4 - f_5 + f_7, \\ c_{12} &= f_3 + f_5, \\ c_{21} &= f_2 + f_4, \\ c_{22} &= f_1 - f_2 + f_3 + f_6, \end{split} $$ where $$ \begin{split} f_1 &= (a_{11} + a_{22}) (b_{11} + b_{22}), \\ f_2 &= (a_{21} + a_{22}) b_{11}, \\ f_3 &= a_{11} (b_{12} - b_{22}), \\ f_4 &= a_{22} (b_{21} - b_{11}), \\ f_5 &= (a_{11} + a_{12}) b_{22}, \\ f_6 &= (a_{21} - a_{11}) (b_{11} + b_{12}), \\ f_7 &= (a_{12} - a_{22}) (b_{21} + b_{22}). \end{split} $$
Fortunately, these formulas hold even if $a_{ij}$ and $b_{ij}$, $i,j=1,2$ are block matrices.
Thus, Strassen algorithm looks as follows.
This leads us again to the divide and conquer idea.
Calculation of number of multiplications is a trivial task. Let us denote by $M(n)$ number of multiplications used to multiply 2 matrices of sizes $n\times n$ using the divide and conquer concept. Then for naïve algorithm we have number of multiplications
$$ M_\text{naive}(n) = 8 M_\text{naive}\left(\frac{n}{2} \right) = 8^2 M_\text{naive}\left(\frac{n}{4} \right) = \dots = 8^{d-1} M(2) = 8^{d} M(1) = 8^{d} = 8^{\log_2 n} = n^{\log_2 8} = n^3 $$So, even when using divide and coquer idea we can not be better than $n^3$.
Let us calculate number of multiplications for the Strassen algorithm:
$$ M_\text{strassen}(n) = 7 M_\text{strassen}\left(\frac{n}{2} \right) = 7^2 M_\text{strassen}\left(\frac{n}{4} \right) = \dots = 7^{d-1} M(1) = 7^{d} = 7^{\log_2 n} = n^{\log_2 7} $$There is no point to estimate number of addtitions $A(n)$ for naive algorithm, as we already got $n^3$ multiplications.
For the Strassen algorithm we have:
since on the first level we have to add $\frac{n}{2}\times \frac{n}{2}$ matrices 18 times and then go deeper for each of the 7 multiplications. Thus,
$$ \begin{split} A_\text{strassen}(n) =& 7 A_\text{strassen}\left( \frac{n}{2} \right) + 18 \left( \frac{n}{2} \right)^2 = 7 \left(7 A_\text{strassen}\left( \frac{n}{4} \right) + 18 \left( \frac{n}{4} \right)^2 \right) + 18 \left( \frac{n}{2} \right)^2 = 7^2 A_\text{strassen}\left( \frac{n}{4} \right) + 7\cdot 18 \left( \frac{n}{4} \right)^2 + 18 \left( \frac{n}{2} \right)^2 = \\ =& \dots = 18 \sum_{k=1}^d 7^{k-1} \left( \frac{n}{2^k} \right)^2 = \frac{18}{4} n^2 \sum_{k=1}^d \left(\frac{7}{4} \right)^{k-1} = \frac{18}{4} n^2 \frac{\left(\frac{7}{4} \right)^d - 1}{\frac{7}{4} - 1} = 6 n^2 \left( \left(\frac{7}{4} \right)^d - 1\right) \leqslant 6 n^2 \left(\frac{7}{4} \right)^d = 6 n^{\log_2 7} \end{split} $$</font>
(since $4^d = n^2$ and $7^d = n^{\log_2 7}$).
Asymptotic behavior of $A(n)$ could be also found from the master theorem.
Total complexity is $M_\text{strassen}(n) + A_\text{strassen}(n)=$ $7 n^{\log_2 7}$. Strassen algorithm becomes faster when
\begin{align*} 2n^3 &> 7 n^{\log_2 7}, \\ n &> 667, \end{align*}so it is not a good idea to get to the bottom level of recursion.
Historically, parallel implementations of many optimized BLAS libraries rely on so-called bulk synchronous programming model:
Let us enumerate elements in the $2\times 2$ matrices as follows
$$ \begin{bmatrix} c_{1} & c_{3} \\ c_{2} & c_{4} \end{bmatrix} = \begin{bmatrix} a_{1} & a_{3} \\ a_{2} & a_{4} \end{bmatrix} \begin{bmatrix} b_{1} & b_{3} \\ b_{2} & b_{4} \end{bmatrix}= \begin{bmatrix} a_{1}b_{1} + a_{3}b_{2} & a_{1}b_{3} + a_{3}b_{4} \\ a_{2}b_{1} + a_{4}b_{2} & a_{2}b_{3} + a_{4}b_{4} \end{bmatrix} $$This can be written as
$$ c_k = \sum_{i=1}^4 \sum_{j=1}^4 x_{ijk} a_i b_j, \quad k=1,2,3,4 $$$x_{ijk}$ is a 3-dimensional array, that consists of zeros and ones:
$$ \begin{split} x_{\ :,\ :,\ 1} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} \quad x_{\ :,\ :,\ 2} = \begin{pmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{pmatrix} \\ x_{\ :,\ :,\ 3} = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{pmatrix} \quad x_{\ :,\ :,\ 4} = \begin{pmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \end{split} $$To get Strassen algorithm we should do the following trick –– decompose $x_{ijk}$ in the following way
$$ x_{ijk} = \sum_{\alpha=1}^r u_{i\alpha} v_{j\alpha} w_{k\alpha}. $$This decomposition is called trilinear tensor decomposition and has a meaning of separation of variables: we have a sum of $r$ (called rank) summands with separated $i$, $j$ and $k$.
Now we have
$$ c_k = \sum_{\alpha=1}^r w_{k\alpha} \left(\sum_{i=1}^4 u_{i\alpha} a_i \right) \left( \sum_{j=1}^4 v_{j\alpha} b_j\right), \quad k=1,2,3,4. $$Multiplications by $u_{i\alpha}$ or $v_{j\alpha}$ or $w_{k\alpha}$ do not require recursion since $u, v$ and $w$ are known precomputed matrices. Therefore, we have only $r$ multiplications of $\left(\sum_{i=1}^4 u_{i\alpha} a_i \right)$ $\left( \sum_{j=1}^4 v_{j\alpha} b_j\right)$ where both factors depend on the input data.
As you might guess array $x_{ijk}$ has rank $r=7$, which leads us to $7$ multiplications and to the Strassen algorithm!
Recent AlphaTensor paper has shown how modern deep reinforcement learning can be used to get new decompositions of tensors.
In reinforcement learning agent learns to make actions based on the state and reward.
In this case, the state is the tensor.
The action is subtraction of a rank-one tensor.
If you get non-zero in the end, you get the reward.
Then, you do millions of different actions, and reinforce good results.
Better ranks for certain matrix sizes
New variants for 4x4 Strassen that work on real hardware faster (but only for this specific hardware!)
Better antisymmetic matrix-by-vector product.
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()