Skolkovo Institute of Science and Technology
Classes: Monday, Tuesday, Thursday 9.00 - 12.00, B2-3006 - B2-3007
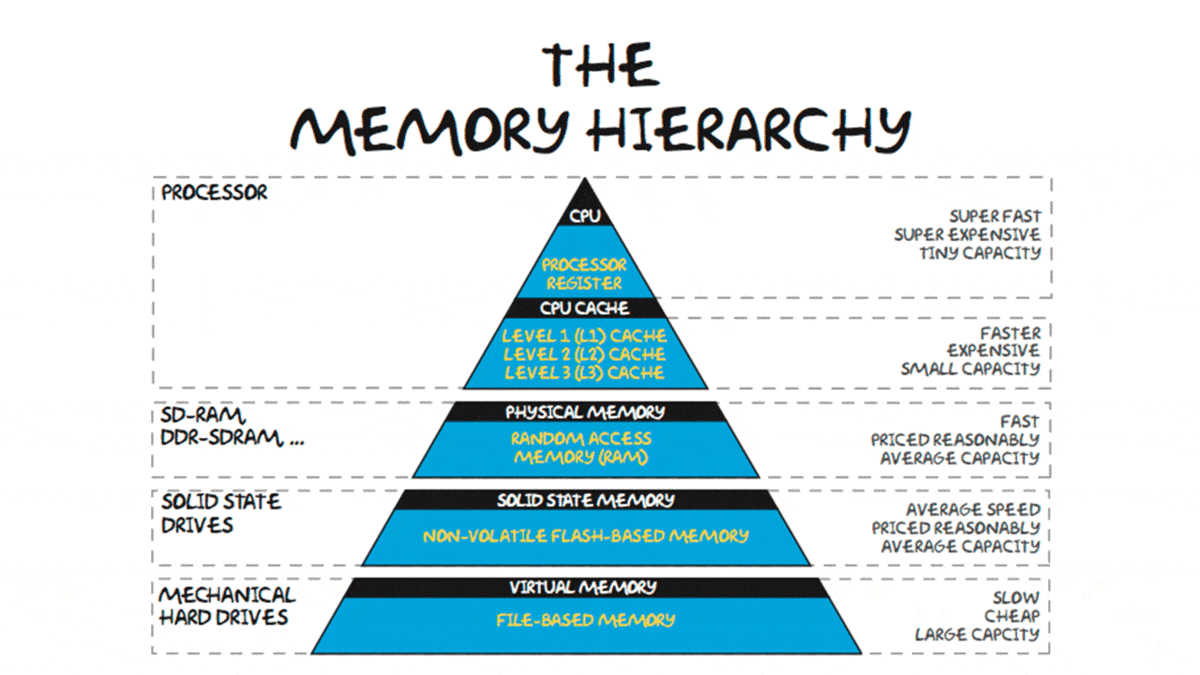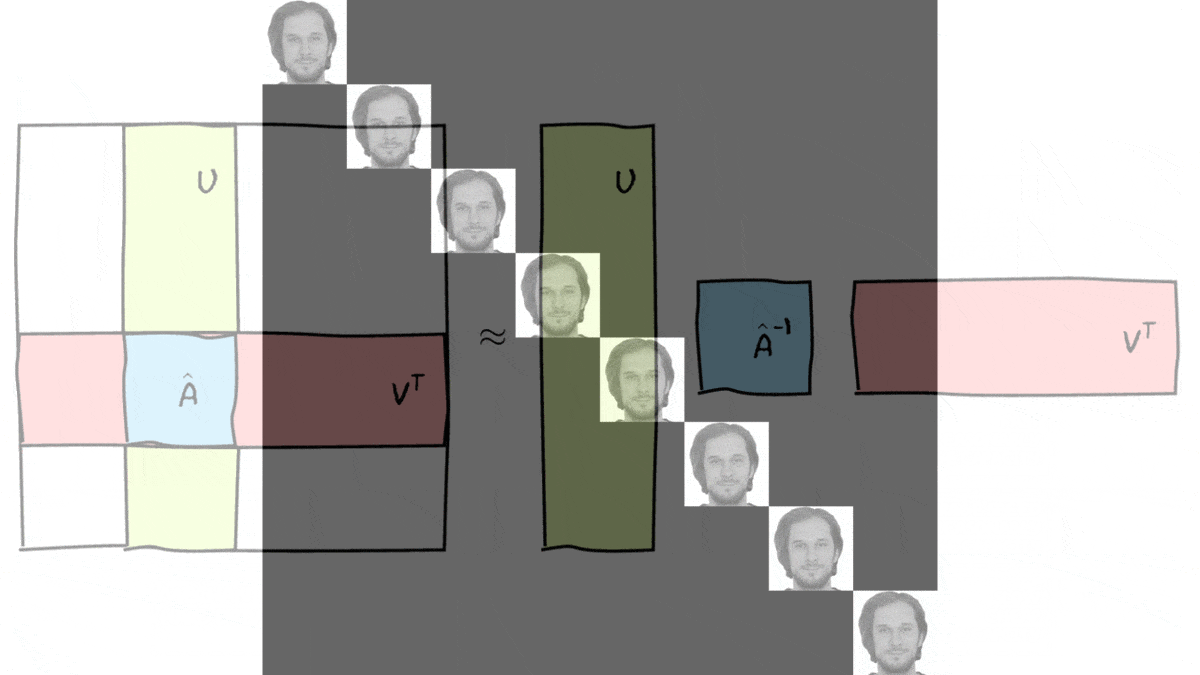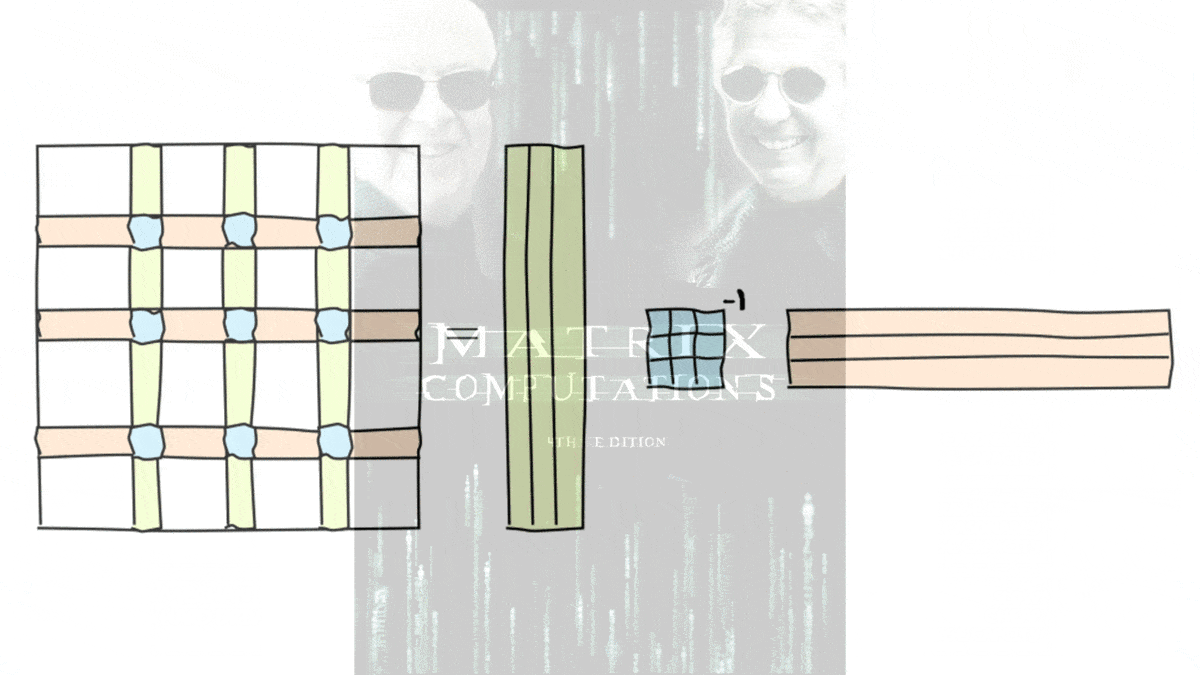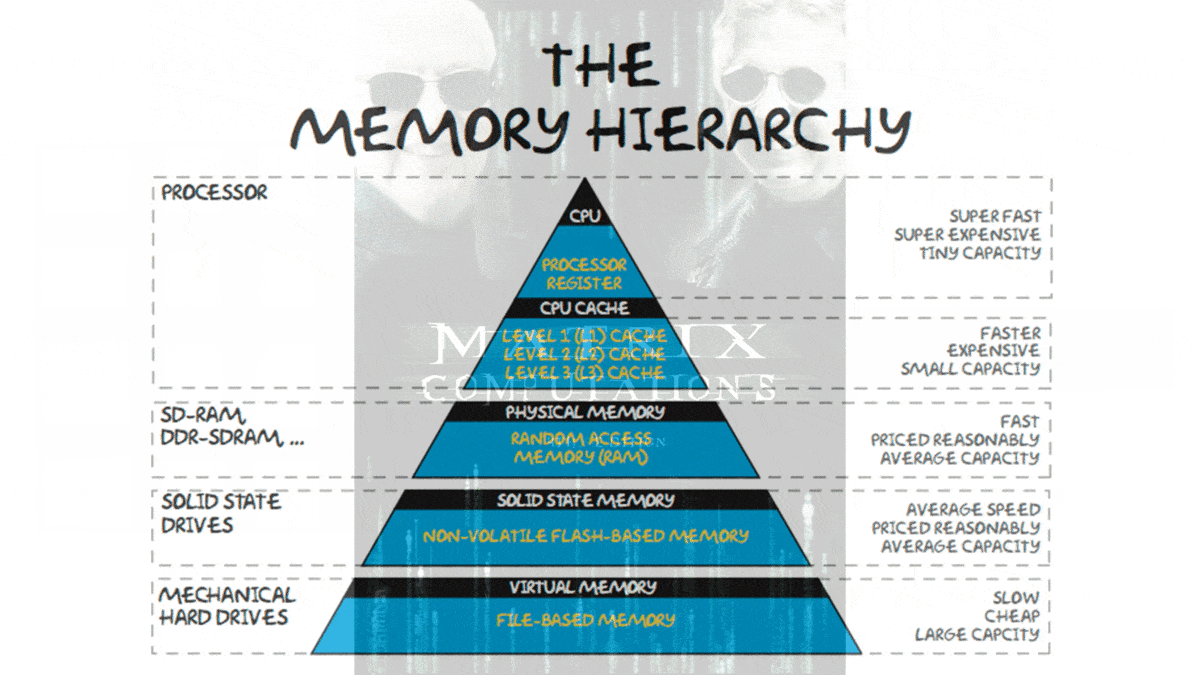
Summary
This is one term course, which provides Skoltech students with basic numerical linear algebra algorithms and ideas. Numerical linear algebra is the basis for computational science, engineering and data science while matrices and their decompositions are the key. The tools are different for small-scale and large-scale problems. We hope, that students after the course will be able to:
- Solve medium-scale numerical linear algebra problems (solve linear systems, compute eigenvalues and eigenvectors, solve linear least squares) using matrix factorizations
- Implement iterative methods for sparse/structured systems
- Find which methods are the most appropriate for the particular problem
- Find appropriate software
Course Materials
- All the materials are available on the site and on the github repo 👽. So, if you found a typo, please, make pull request to the repo!
- Matrix decomposition cheat sheet
If you have difficulties with basic linear algebra:
- Cheat sheet with basics
- Gilbert Strang book "Introduction to Linear Algebra"
- Gilbert Strang has recorded lectures on YouTube
Comprehensive NLA books:
- Gene H. Golub, Charles. F. Van Loan, "Matrix computations" (4th edition)
- Lloyd N. Trefethen and David Bau III, "Numerical Linear Algebra"
- Eugene. E. Tyrtyshnikov, "Brief introduction to numerical analysis"
- James W. Demmel, "Numerical Linear Algebra"
Many applications of linear algebra you can find in "Introduction to Applied Linear Algebra" by S. Boyd and L. Vandenberghe
Instructor:

Assistants:

Katrutsa

Rudenko

Merkulov

Cherniuk

Sevriugov

Mezentsev

Daulbaev